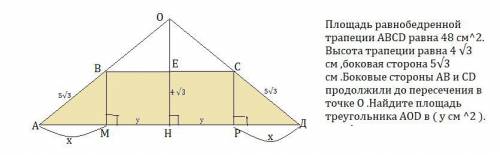
Площадь равнобедренной трапеции ABCD равна 48 см². Высота трапеции равна 4√3 см ,боковая сторона 5√3 см .Боковые стороны AB и CD продолжили до пересечения в точке О .Найдите площадь треугольника AOD в ( у см² ).
Объяснение:
1) Пусть МВ⊥АД, СР⊥АД. Тогда ΔАВМ=ΔДСР как прямоугольные по гипотенузе (АВ=СД) и острому углу (∠А=∠Д , как углы при основании равнобедренной трапеции)⇒ АМ=РД .
2)ΔАВМ-прямоугольный , по т. Пифагора АМ=√(25*3-16*3)=3√3 (см), значит РД=3√3 см.
3)Длина АД=АМ+МР+РД=6√3+МР . Пусть МН=у, АД=6√3+2у ⇒ВС=6√3+2у .
S(трап)=1/2*(АД+ВС)*ЕН , 48=1/2*(6√3+4у)*4√3 ,6√3+4у=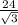 
,
4у= 8√3-6√3 , у=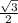 
⇒ ВЕ=
4) АН=3√3- 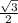=3,5√3 (см).
ΔОВЕ подобен ΔОАН по двум углам: ∠О-общий,∠ВЕО=∠АНО=90°, значит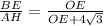 
, 
, 
,
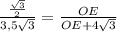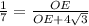OE=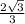 
см
5) Высота ОН= 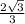+4√3 = 
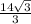(см) , АД=6√3+√3=7√3 (см).
S(AOД)=1/2*АД*ОН , S(AOД=1/2* 7√3* 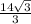= 49(см²).
Сумма углов треугольника равна 180 градусов. Если углы треугольника относятся как 5 : 6 : 7, то это значит, что первый угол содержит 5 частей, второй - 6 таких же частей, а третий 7 таких же частей градусных мер угла.
Пусть одна часть угла равна х градусов, тогда первый угол треугольника равен 5х градусов, второй угол равен 6х градусов, а третий угол - 7х градусов. По условию задачи известно, что сумма углов треугольника равна (5х + 6х + 7х) градусов или 180°. Составим уравнение и решим его.
5х + 6х + 7х = 180;
18х = 180;
х = 180 : 18;
х = 10° - градусная мера одной части;
5х = 10° * 5 = 50° - первый угол;
6х = 10° * 6 = 60° - второй угол;
7х = 10° * 7 = 70° - третий угол.
Все углы треугольника острые, значит, этот треугольник будет остроугольным.
ответ. 50°, 60°, 70°
Объяснение: