ответ: 9 см, 25 см, 255 см²
Объяснение:
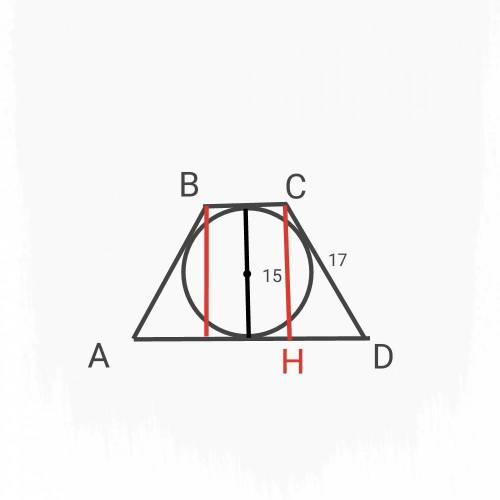
Пусть меньшее основание BC, большее - AD.
Известно, что диаметр окружности равен 15, проведем его от нижнего основания трапеции до верхнего - получится высота трапеции.
Независимо от того, куда мы двигаем высоту, она остается неизменной:
Проведем высоту из левого и правого концов нижнего основания. Получится прямоугольный треугольник (см. картинку).
СD = 17 по усл., CH (назовем так наш перпендикуляр из точки C) = 15. Находим HD по т.Пиф. = 17² - 15² = 8.
Аналогично с левой стороной.
Отметим меньшее основание за х, тогда большее основание = 8+х+8 = 16+х.
Мы знаем, что сумма противоположных сторон четырехугольника, в который вписана окружность, равна сумме других противоположных сторон.
АВ + СD = BC + AD
34 = 2х + 16
2 х = 34 - 16
х = 9 см (т.е меньшее основание = 9)
Большее основание = х + 16 = 9 + 16 = 25 см.
S = 1/2 * (BC + AD)* CH = 17 * 15 = 255 см²
\begin{gathered} 3\cos 2x = 7\cos x \\ 3(2\cos ^{2}x - 1) - 7\cos x = 0 \\ 6\cos ^{2}x - 3 - 7\cos x = 0 \\ \cos x = t \\ 6t^{2}-7t-3=0 \\ D = 49 + 24*3 = 121 \\ \\ t_{1} = \dfrac{7 + 11}{12} = 1.5 \ ; \ \ \ t_{2} = \dfrac{7-11}{12} = -\dfrac{1}{3} \\ \\ $\left[ < br / > \begin{gathered} < br / > \cos x = 1.5 \\ \cos x = -\dfrac{1}{3} \\ < br / > \end{gathered} < br / > \right.$ \ \ \ ; \ < br / > $\left[ < br / > \begin{gathered} < br / > x \notin [-1;1] \\ x = \pm \arccos( -\dfrac{1}{3}) + 2\pi n, n \in Z < br / > \end{gathered} < br / > \right.$ \end{gathered}
ответ: Ух-ты, много чего надо решить, но это просто, держи:
Угол при вершине - 144, углы при основании - по 18.
Внешний угол при вершине - 36. Внешние углы при вершинах основания - 162.
Объяснение:
8х+х+х=180
10х=180
х=18 - Углы при основании.
8х=18*8=144 - Угол при вершине.
1 Внешний угол - 180-144=36.
2 Внешний угол - 180-18=162.
3 Внешний угол - 180-18=162.
Удачи!