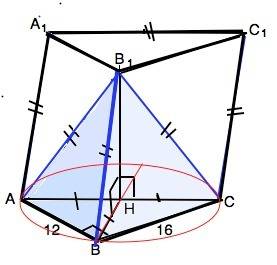
Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
105=15+90.
1)Строим прямоуг. треуг-к АОС , с углом С 60 градусов
(строим 2 перпенд.прямых а и б, на а от О - точки пересечения прямых - откладываем ОА. От точки А окладываем на прямую а дальше это же расстояние - АД. Теперь из точки А строим окружность с радиусом ОД, что равно 2 ОА.Точку пересечения окружности и прямой б назовём С. В прямоугольном треугольнике АОС угол А =60 градусов, С=30 градусов). отрезок АС назовём с.
2)Проводим биссектрису угла С.
3)строим к ней перпендикуляр д через точку С. берём угол этого перпендикуляра, в котором внутри лежит точка О. Прибавляем к нему угол дс. 90+15(т.к. угол АСО 30 градусов, строили биссектрису) =105.
От любого выпуклого 4угольника можно отрезать треугольник так, чтобы получилась трапеция. Для этого надо из вершины провести линию II стороне, с которой у неё нет общих точек. Если такая линяя идет снаружи - проводим прямую II другой стороне. Или выбираем другую вершину. Всего вариантов 8 (из каждой вершины по 2 линии, II каждой из 2 противоположных сторон), и хотя бы один такой разрез найдется (теоретически это требует строгого доказательства :.
Ну, а от трапеции всегда можно отрезать треугольник, чтобы получился параллелограмм. Тут и доказывать нечего :)))
Получается, что любой выпуклый 4угольник подходит.
Я не стал доказывать первое утверждение - это много места займет, как мне кажется :)) Звучит оно так.
Надо доказать, что если в выпуклом 4 угольнике провести из каждой вершины прямые, параллельные противоположным сторонам, то ХОТЯ БЫ одна такая прямая пересечет ДРУГУЮ противоположную сторону ВНУТРИ 4угольника. (Стороной, противоположной вершине, считается та, у которой эта вершина не является концом.)