Обозначим первый угол треугольника через х.
Второй угол треугольника в три раза больше первого. Значит величина второго угла 3х.
Он же должен быть на пять градусов меньше третьего. Значит Третий угол на пять градусов больше второго. Величина третьего угла: 3х+5°.
Сумма трех углов в треугольнике 180°.
Составляем уравнение:
х+3х+3х+5°=180°
7х=180°-5°
7х=175°
х=175°:7
х=25°
Первый угол в треугольнике 25°.
Второй угол в треугольнике: 3х=3*25°=75°.
Третий угол в треугольнике: 3х+5°=75°+5°=80°.
ответ: 25°, 75°, 80°.
Объяснение:
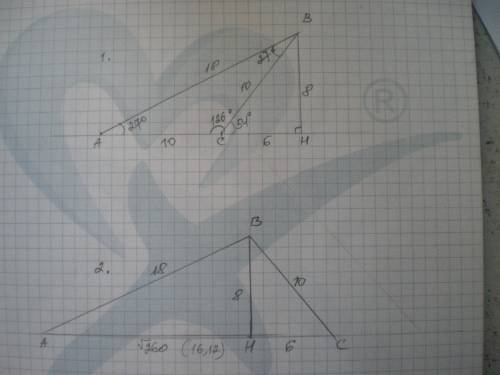
Задача имеет 2 решения.
1. Наклонные проведены по одну сторону от перпендикуляра.
Имеем прямую АН, ВН⊥АН, ВН=8 см, ВС=10 см, АВ=18 см. Найти АС.
ΔВСН - прямоугольный, ВН=8 см, ВС=10 см, тогда СН=6 см (египетский треугольник).
По теореме синусов sin∠ВСН=8\10, ∠ВСН=54°.
∠АСВ=180-54=126°.
Найдем ∠А из ΔАВС.
sin126\АВ=sinА\ВС; sinА=0,809*10:18=0,4494; ∠А=27°
∠АВС=180-126-27=27°, значит,ΔАВС - равнобедренный и АС=ВС=10 см. ответ 10 см.
2. Наклонные проведены по обе стороны от перпендикуляра.
Дано: АС⊥ВН; ВН=8 см, АВ=18 см, ВС=10 см. Найти АС.
В ΔВСН СН=6 см (египетский треугольник), АН найдем по теореме Пифагора:
АН=√(АВ²-ВН²)=√(324-64)=√260≈16,12 см.
АС=16,12 + 6 = 22,12 см.
ответ: 22,12 см.
Пусть одна сторона x , а вторая x+2
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон
Имеем
8**2+14**2=2(x**2+ (x+2)**2)
260=4x**2+8x+8
-4x**2-8x+252=0
Сократим на -4
x**2+2x-63=0
Найдём дискриминант
D=2**2+63*4=4+252=256
Корень из дискриминанта 16
Найдём x
x1= (-2+16)/2=7
x2=(-2-16)/2=-9
Так как сторона не может быть отрицательным числом - ответ 7
Вторая сторона 7+2=9
Найдём периметр
P=2(a+b)= 2(7+9)=32 см