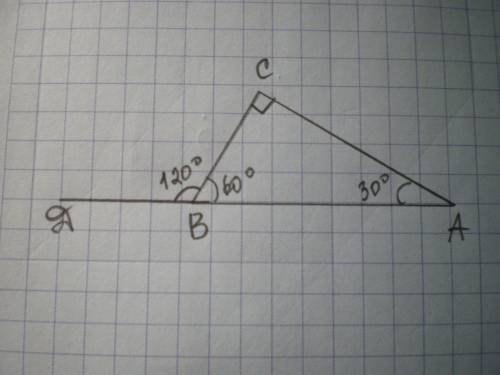
Дано: ΔАВС - прямоугольный, ∠С=90°, ∠ДВС=120°, АВ+ВС=24 см.
Найти АВ, ВС.
По свойству смежных углов ∠ДВА+∠СВА=180°, тогда
∠СВА=180-∠ДВС=180-120=60°.
По свойству острых углов прямоугольного треугольника
∠А=90-∠СВА=90-69=30°
В треугольнике против большей стороны лежит больший угол, поэтому АВ - большая сторона. Против меньшей стороны лежит меньший угол, поэтому ВС - меньшая сторона.
ВС=1\2 АВ по свойству катета, лежащего против угла 30°.
Составим уравнение: АВ+1\2 АВ = 24; 1,5 АВ = 24; АВ=16 см.
ВС=16:2=8 см.
ответ: 8 см, 16 см.
ответ: переведено с программы-переводчика, русская оригинальная версия в объяснении
(Точка М на малюнку відповідає точці E в даній задачі)
Так як бісектриса кута паралелограма відсікає від нього рівнобедрений трикутник, то АВ = ВЕ = 7 см
У параллелограмме всі сторони попарно рівні і паралельні.
З цього випливає, що AD = ВС = 12 см
ЕС = ВС - ВЕ = 12 - 7 = 5 см
Відповідь: BE = 7 см і EC = 5 см
Объяснение:
(Точка М на рисунке соответствует точке E в данной задаче)
Так как биссектриса угла параллелограмма отсекает от него равнобедренный треугольник, то АВ = ВЕ = 7 см
В параллелограмме все стороны попарно равны и параллельны.
Из этого следует, что AD = ВС = 12 см
ЕС = ВС - ВЕ = 12 - 7 = 5 см
ответ: BE = 7 см и EC = 5 см