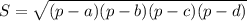Только потому, что налажал в комментариях.
См. чертеж.
1) строится заданный угол φ, на чертеже это угол с вершиной в точке K. Проводится биссектриса и перпендикулярная ей прямая KE. Строится в общем произвольный отрезок BE, концы которого расположены как на чертеже.
Смысл в том, что из точки K отрезок BE виден под углом 90° + φ/2.
2) на отрезке BE от точки B откладывается заданная сторона a, получается точка C. Проводится CG II KE.
Теперь заданная сторона BC = a видна из точки G под углом 90° + φ/2.
3) строится описанная окружность треугольника BCG.
Эта процедура всем известна, я её на чертеже не отображаю, тем более, что GeoGebra строит её автоматически.
4) от точки C во вне отрезка BC откладывается заданная разность d, получается точка D, то есть CD = d. Отрезок BD делится пополам, так находится точка J (то есть BJ = JD).
5) из точки J проводится перпендикуляр к BC до пересечения с окружностью (BGC) в точке I.
I - центр вписанной окружности искомого треугольника
6) проводится окружность с центром I и радиусом IJ.
вписанная окружность.
7) проводятся две окружности - с центром B и радиусом BJ и центром в C и радиусом CJ. Так находятся точки пересечения этих окружностей с вписанной окружностью - точки F и H.
Они же - точки касания боковых сторон.
8) проводятся BF и CH до пересечения в точке A.
ABC - искомый треугольник.
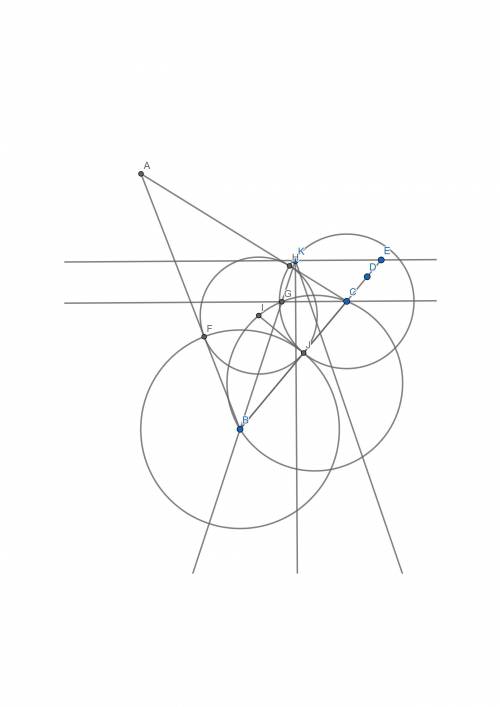
16.
а)
Диагональ BD — делит четырёхугольник на 2 произвольных треугольника: ΔBCD; ΔBAD.
Проведём также диагональ CA: он проходит через ΔBCD.
ΔBCD — равнобёдренный, так как:
А в свойствах равнобёдренного треугольника входит то, что высота, медиана, и биссектриса, проведённая с вершины к основанию — одно и то же, что и означает, что наш отрезок CO — медиана, и поэтому делит диагональ BD — на 2 равные части.
б)
Я не вижу в этом варианте заданное условие. А если она и вправду есть, то найти площадь, зная то, что отрезки являются "целыми числами", я не смогу.
Но площадь четырёхугольника можно найти — зная всего-лишь его стороны: