Сумма углов треугольника равна 180°. Так как углы при основании равнобедренного треугольника равны, то угол при вершине равен 180° - 2*30° = 180 - 60 = 120°.
Площадь треугольника равна:
S = 0.5 * AB * BC * sinB = 0.5 AB²sin120°, где AB = BC как боковые стороны.
Тогда AB² = 2S/sin120° = 2*4√3/(√3/2) = 16 ⇒ AB = 4
Теперь рассмотрим прямоугольный треугольник, который образован искомой высотой, одной из боковой сторон и половиной длины основания. Угол, противолежащий искомой высоте, равен 30° по условию. Тогда, по определению синуса, h = AB*sin30° = 4 * 0.5 = 2.
ответ: 2
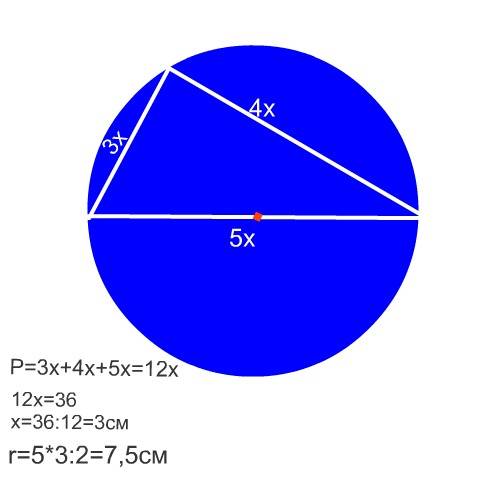
Гипотенуза этого прямоугольного треугольника является диаметром окружности.
Так как отношение катетов 3:4, то гипотенуза в этом отношении будет 5,
т.е все стороны треугольника относятся как 3:4:5, поскольку этот треугольник - египетский.
Примем коэффициент отношения сторон за х
тогда его периметр равен
3х+4х+5х=12х
Коэффициент равен 36:12=3
Диаметр круга
3*5=15 см
Радиус 15:2=7,5 см
-------------------------------
Боковую сторону можно найти через синус угла при вершине треугольника.
Он равен 180-2а
х=h: sin(180-2а)
ответ:12см
Объяснение:BK=NB=3см, КА=PA=12cм (как касательные что выходят из одной точки)
BA=BK+KA=15см
NB=PF=3см
FA=PA-PF=9см
Рассмотрим треугольник BFA, угол BFA=90°
За теоремой Пифагора: BA^2=BF^2+FA^2
BF=√BA^2-FA^2=√225-81=√144=12см