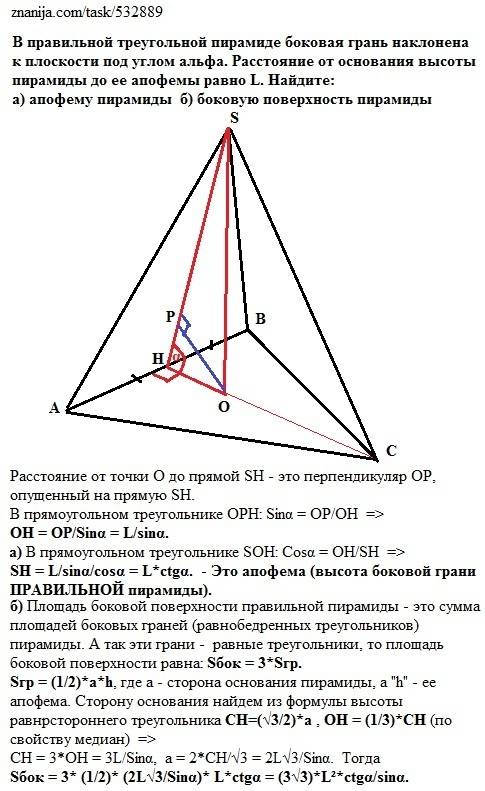
Нам дана правильная пирамида. Значит ее основание - правильный треугольник, а боковые грани - равные равнобедренные треугольники. Кроме торго, вершина пирамиды проецируется в центр основания - точку О пересечения медиан (высот и биссектрис правильного треугольника) основания.
Высота боковой грани правильной (и только правильной!) пирамиды называется ее АПОФЕМОЙ.
Расстояние от точки О до прямой SH (апофема) - это перпендикуляр ОР, опущенный из точки О на прямую SH.
В прямоугольном треугольнике ОРН: Sinα = OP/OH =>
ОН = ОР/Sinα = L/sinα.
а) В прямоугольном треугольнике SОН: Cosα = OH/SH =>
SH = L/sinα/сosα = L*ctgα. - Это апофема (высота боковой грани ПРАВИЛЬНОЙ пирамиды).
б) Площадь боковой поверхности правильной пирамиды - это сумма площадей боковых граней (равнобедренных треугольников) пирамиды. А так как эти грани - равные треугольники, то площадь боковой поверхности равна: Sбок = 3*Sгр.
Sгр = (1/2)*а*h, где а - сторона основания пирамиды, а "h" - ее апофема. Сторону основания найдем из формулы высоты равнрстороннего треугольника СН=(√3/2)*а . Отрезок ОН = (1/3)*СН (по свойству медиан) =>
CH = 3*OH = 3L/Sinα, a = 2*CH/√3 = 2L√3/Sinα. Тогда
Sбок = 3* (1/2)* (2L√3/Sinα)* L*ctgα = (3√3)*L²*ctgα/sinα.
Легко найти сторону ромба, четверть ромба - это египетский треугольник (8,15,17).
Поэтому боковая сторона 17, а угол BDM = g, sin(g) = 15/17, cos(g) = 8/17. (Так проще, чем все время писать arcsin...)
В треугольнике BDM стороне DM противолежит (:)) угол DBM, у которого sin(DBM) = 1/2, то есть это pi/6. Это понятно, поскольку это угол между линией ВО и касательной из В, а ВО в 2 раза больше радиуса.
Далее применяем теорему синусов к треугольнику DBM.
(напомню, что sin(pi - g) = sin(g))
DM/sin(pi/6) = DB/sin(pi/6 + g)
DM = 8/((1/2)*(8/17) + (корень(3)/2)*(15/17)) = 272/(8+15*корень(3));
(между прочим, это почти точно 8, а точнее, 8,00452912419152, это можно было предвидеть - угол g очень близок к 60 градусам, а точнее, g примерно 61,927513064147 градусов. Поэтому треугольник DBM очень близок к прямоугольному.)
Само собой, СМ = 17 - 272/(8+15*корень(3));
это можно записать в такой "красивой" форме
СМ = 17*(1 - х)/(1 + х); где х = 8/(15*корень(3))
Продолжая традицию, скажу, что х почти точно 0,3 (еще точнее, - 0,3079201435678)