1)Геометрическое преобразование плоскости — взаимно-однозначное отображение этой плоскости на себя. Наиболее важными геометрическими преобразованиями являются движения, т. е. преобразования, сохраняющие расстояние.
2)
Преобразование плоскости (или пространства), при котором сохраняется отношение расстояний, называется преобразованием подобия или просто подобием. Другими словами, при преобразовании подобия F для любых двух точек имеет место соотношение F(A)F(B) = kAB, где k – некоторое число, называемое коэффициентом подобия.
3)
Две фигуры называют гомотетичными, если одна из них переходит в другую при некоторой гомотетии. Из определения следует, что при $k=-1$ гомотетия является центральной симметрией с центром в точке $O$, а при $k=1$ — тождественным преобразованием
4)Гомоте́тия (от др.-греч. ὁμός «одинаковый» + θετος «расположенный») — преобразование плоскости (или пространства), заданное центром O и коэффициентом {\displaystyle k\neq 0}k\neq 0, переводящее каждую точку {\displaystyle X}X в точку {\displaystyle X'}X' такую, что {\displaystyle {\overrightarrow {OX'}}=k{\overrightarrow {OX}}}\overrightarrow {OX'}=k\overrightarrow {OX}. При этом центр остаётся на месте. Гомотетию с центром O и коэффициентом k часто обозначают через Н^k O
меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
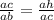
теперь подставим наши значения в эту пропорцию:
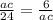
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см

15 см будут высоти,потому что 150градусов кут