Катет прямокутного трикутника дорівнює а, а прилеглий кут а. Знайдіть площу бічної поверхні тіла, утвореного при обертанні цього трикутника навколо даного катета.
Найдем, какую часть площади искомых треугольников составляют от площади треугольника АВС:
Медиана делит треугольник на два равновеликих, значит S (ABM) = S (CBM) = 1/2 S (ABC) (1)
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам и Площади треугольников, имеющих общую высоту, относятся, как стороны, к которым проведена высота (доказательство на нижнем рисунке).
АР - биссектриса ΔАВС, ⇒ BP : PC = AB : AC = 1 : 3 Треугольники АВР и АСР имеют общую высоту, проведенную из вершины А, поэтому отношение их площадей: S (ABP) : S (ACP) = BP : PC = 1 : 3, т.е S (ABP) = 1/4 S (ABC)
АР - биссектриса и треугольника АВМ, значит BK : KM = AB : AM = 1 : (3/2) = 2 : 3 (так как АМ = 1/2 АС) Треугольники АВК и АМК имеют общую высоту, проведенную из вершины А, значит: S (ABK) : S (AMK) = BK : KM = 2 : 3, т.е. S (ABK) = 2/5 S (ABM) = 1/5 S (ABC) ( с учетом (1) ) S (AMK) = 3/5 S (ABM) = 3/10 S (ABC)
S(BKP) = S (ABP) - S (ABK) = 1/4 S (ABC) - 1/5 S (ABC) = 1/20 S (ABC)
Объяснение:
Смотри прикреплённый рисунок.
О - точка пересечения медиан АМ и BN.
Медианы треугольника точкой пересечения О делятся в отношении 2:1, считая от вершины, поэтому BO =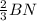
= 2 см, NO = 
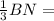1 cм.
Проведём линию MN, соединяющую середины сторон АС и ВС.
MN = 0.5AB, поскольку MN - средняя линия треугольника.
ΔNMC ~ ΔABC по двум углам (∠С - общий, ∠СMN = ∠СBA как соответственные при MN || AB и секущей ВС)
Коэффициент подобия k = MN: AB = 0,5, поэтому площади ΔNMC и ΔABC относятся, как k² = 0.25.
Тогда площадь трапеции ABMN составляет 0,75 площади ΔABC.
Вычислим площадь трапеции ABMN.