Прямая, содержащая высоту равнобедренного треугольника, является и его медианой, следовательно, она является срединным перпендикуляром к хорде, и поэтому проходит через центр окружности. Обозначим исходный треугольник через ABC (AC - основание), через M - середину AC, через O - центр окружности. В прямоугольном треугольнике BOC высота CM является средним пропорциональным проекций катетов на гипотенузу, поэтому |MO| = |MC|2/|BM| = 16/3. Из прямоугольного треугольника OCM по теореме Пифагора получаем, что |OC|2 = |OM|2+|MC|2 = (20/3)2. или =
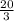
треугольник MDK, MD - Основание, из углов при основании проведем высоты МH и DF, точка пересечения высот О, угDMН=угFDM=(180-160)/2=10
уг.FOM=уг.DОН=180-160=20 уг.KMН=уг.KСF=90-20=70 (рассмотри треуг-ки АМО И СОН, следовательно углы при основании треугольника равны уг.KMН+уг.DMН = 10 +70 = 80, а уголл, противолежащий основанию равен 180-80*2=50
Объяснение: