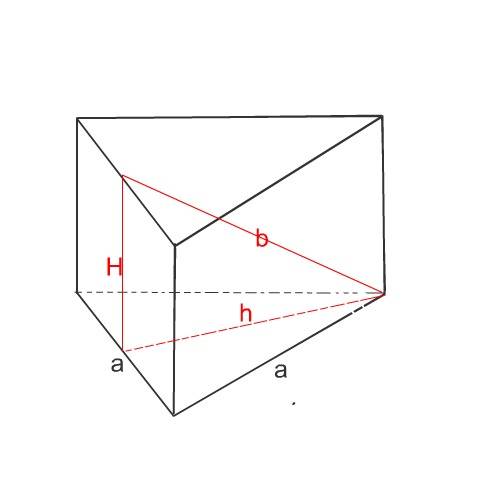
Картинка в этой задаче действительно желательна.
Объем правильной треугольной призмы равен произведению площади основания на высоту призмы.
Площадь основания - это площадь правильного треугольника со стороной а.
Формула площади равностороннего треугольника
S=(a²√3):4
Высоту призмы найдем из прямоугольного треугольника,
катеты в котором- высота призмы и высота треугольника=основания,
а гипотенуза - данное в условии расстояние b от вершины одного основания до противолежащей стороны другого основания.
Высота правильного треугольника находится по формуле
h=а√3):2
Высоту призмы найдем по теореме Пифагора:
Н= √(b²-h²)=√(b²-3а²:4)
V= (a²√3):4)·√(b²-3а²:4)
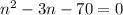
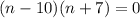
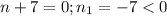 - не подходит, количество вершин не может быть отрицательным
- не подходит, количество вершин не может быть отрицательным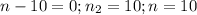
Простецко. Решение с одной очень крутой теоремы: если хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков второй хорды: Обозначим один отрезок через х, значит второй отрезок будет 5-х
6*1=х*(5-х)
6=5х-х²
х²-5х+6=0
получается квадратное уравнение
находим дискриминант
Дискриминант положительный, значит всё идёт верно:
Первый корень равен 2, следовательно, второй корень равен 3
окончательный ответ: 2 и 3 см