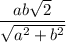Так, подібні. У ромба всі сторони рівні. Якщо провести меншу діагональ, то ми отримаємо ромб, який складається з двох правильних (рівносторонніх) трикутників. Будь-які правильні трикутники подібні (за трьома сторонами). Тому подібними є і конструкції з двох таких трикутників.
P. S. Якщо вже доводити максимально строго: у правильного трикутника кут дорівнює 60°. Тому в цього ромба кути дорівнюють 120°, 60°, 120°, 60°, а всі сторони рівні. Якщо у двох чотирикутників рівні всі відповідні кути, а відповідні сторони пропорційні, то вони подібні.
Пусть дан треугольник АВС с прямым углом А, в котором проведена биссектриса АЕ, длину которой нужно найти.
Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.
Запишем пропорцию:
Пусть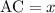 . Тогда
. Тогда 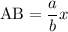 .
.
Запишем теорему Пифагора для треугольника АВС:
Значит:
Запишем теорему синусов для треугольника АЕС:
Так как АЕ - биссектриса, то ЕАВ и ЕАС равны по половине прямого угла, то есть по 45°.
Синус угла С определим как отношение противолежащего катета к гипотенузе:
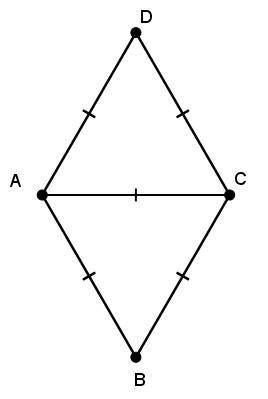
Теперь можем найти биссектрису:
ответ: