Давай найдём площадь треугольника за формулой Герона
S=√p(p-a)(p-b)(p-c), где p -пол периметра, аbc стороны треугольника
S=√ 30 × 20 × 6 × 4 = √ 6×5×5×4×6×4 =
120 ( 30 и 20 разложил на меньшие числа)
Радиус вписаной окружности в разносторонним треугольнике ищется за формулой r = S/p, p - пол периметра
r = 120/30=4 см
Площадь круга:
S = πR² = 16π
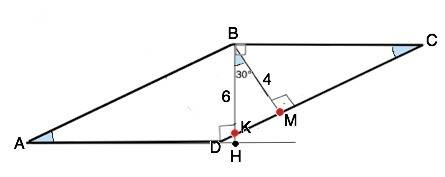
ВМ ⊥ CD, но ВН не является гипотенузой прямоугольного треугольника, образованного высотами, т.к. ВМ:ВН =4/6, и это отношение не равно cos30°
ВН пересекает СD в т.К.
∆ ВКМ - прямоугольный, угол МВК=30°, след, угол ВКМ=60°. Тогда в подобном ему по общему острому углу при К прямоугольном ∆ ВКС
угол ВСК=30°
Катет ВМ противолежит углу 30°, след. гипотенуза ВС=2 ВМ=8 см.
В параллелограмме противоположные углы равны.
След. ∠ВАН=BAD=30°, и катет ВН противолежит углу 30°, ⇒ гипотенуза АВ=2 ВН=12 см.
Площадь параллелограмма равна произведению высоты на сторону, к которой проведена.
CD=AB=12 см
S= CM•CD=4•12=48 см²
* * *
Или
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними:
S=a•b•sinα
S=12•6•sin30°=96•1/2=48 см
120 см
Объяснение: