Площадь полной поверхности прямоугольного параллелепипеда
равна сумме площадей 6 прямоугольников, его образующих.
Площадь двух прямоугольников, со сторонами 6 и 12 = 6*12 = 72 кв.ед
Обозначим третью сторону параллелепипеда за x, тогда
S(полн. пов) = 2(72+6x+12x)
2(72+6x+12x) = 576
144 + 36х = 576
36х = 432
x = 12
Длина диагонали прямоугольного параллелепипеда равна корню суммы квадратов трёх его измерений.
d =
Предположим, что мы не знаем данное свойство, тогда мы найдём диагональ основания параллелепипеда со сторонами 6 и 12 исходными. Т.к, параллепипед прямоугольный, то по теореме Пифагора следует, что
d1 = . Можно не считать, а пока оставить так.
Найдём теперь диагональ параллелепипеда. Найденная диагональ является проекцией диагонали параллелепипеда на его основание.
Чтобы её найти, мы берём третью сторону (высоту параллелепипеда) и найденную диагональ. Также, по т. Пифагора находим диагональ параллелепипеда d2
если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой. Доказательство: пусть а 1 и а 2 - две параллельные прямые и a - плоскость, перпендикулярная прямой а 1 . lib.com.ru/Exact Science/ma_a1.htm
Свойство перпендикулярной прямой и плоскости
Пусть a1 и a2 – две параллельные прямые и α - плоскость, перпендикулярная прямой a1. Докажем, что эта плоскость перпендикулярна и прямой a2. Проведем через точку A2 пересечения прямой a2 с плоскостью α произвольную прямую...
Проекция это когда опускаешь перпендикуляр из точки конца отрезка ты проводишь высоту из вершины В к основанию АС и находишь отрезочки на которые делится основание этой высотой а еще нужно заметить что треугольник АВС прямоугольный и можно найти АС АС в квадрате = 20*20+15*15 ас в квадрате=625 Ас =25 вот есть у тебя треугольник там есть подобные треугольники маленький треугольник подобен большому я возьму что точка где будет заканчиваться проекция Н вот получается что треугольник АВН подобен АВС и можно использовать отношение сходственных сторон 20\25=х\15 х это АН потом из 25 вычитаешь полученное и все)
Площадь полной поверхности прямоугольного параллелепипеда
равна сумме площадей 6 прямоугольников, его образующих.
Площадь двух прямоугольников, со сторонами 6 и 12 = 6*12 = 72 кв.ед
Обозначим третью сторону параллелепипеда за x, тогда
S(полн. пов) = 2(72+6x+12x)
2(72+6x+12x) = 576
144 + 36х = 576
36х = 432
x = 12
Длина диагонали прямоугольного параллелепипеда равна корню суммы квадратов трёх его измерений.
d =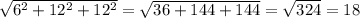
Предположим, что мы не знаем данное свойство, тогда мы найдём диагональ основания параллелепипеда со сторонами 6 и 12 исходными. Т.к, параллепипед прямоугольный, то по теореме Пифагора следует, что
d1 =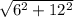 . Можно не считать, а пока оставить так.
. Можно не считать, а пока оставить так.
Найдём теперь диагональ параллелепипеда. Найденная диагональ является проекцией диагонали параллелепипеда на его основание.
Чтобы её найти, мы берём третью сторону (высоту параллелепипеда) и найденную диагональ. Также, по т. Пифагора находим диагональ параллелепипеда d2
d2 =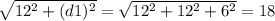
Отсюда и вытекает свойство о трёх измерениях.
ОТВЕТ: 18