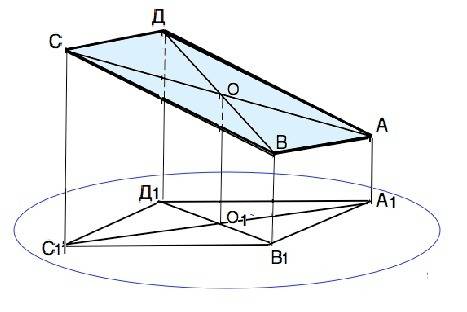
Проекция точки на плоскость есть точка пересечения с плоскостью прямой, проходящей через данную точку перпендикулярно к данной плоскости. Перпендикулярные прямые, проведенные к одной и той же плоскости, параллельны. ⇒ Отрезки перпендикулярных прямых от вершин параллелограмма к плоскости взаимно параллельны. В четырехугольнике АА1С1С стороны АА1|║СС1, в четырехугольнике ВВ1ДД1 стороны ВВ1║ДД1. В выпуклых четырехугольниках АА1С1С и ВВ1Д1Д две стороны параллельны, они – трапеции по определению.
Проведем в параллелограмме и его проекции диагонали. Точки их пересечения обозначим О и О1 соответственно. Диагонали параллелограмма точкой пересечения делятся пополам. Следовательно, ОО1 - средняя линия трапеций АА1С1С и ВВ1Д1Д. Тогда ОО1=(АА1+СС1):2= 10:2=5 м. Поэтому ВВ1+ДД1=2•ОО1=10. ⇒ДД1=10-3=7 м.

21°
Объяснение:
Пусть ∠Д равен х. Тогда ∠В=0,3х, а ∠Е=х+19.
Сумма углов треугольника равна 180°.
х+0,3х+х+19=180
2,3х=161
х=70
∠Д=70°
ТОгда ∠В=0,3х=21°