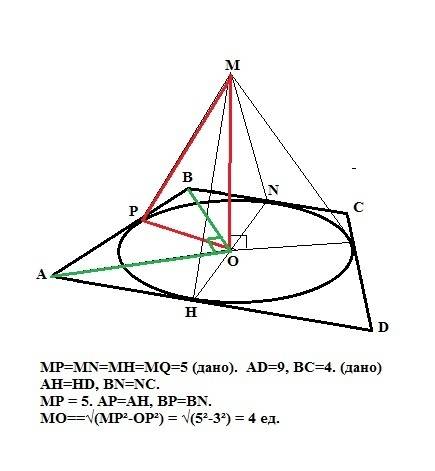
Пусть дана равнобедренная трапеция АВСD. Из условия ясно, что точка М проецируется в центр О вписанной в трапецию окружности, так как расстояние от точки М до стороны - это перпендикуляр из точки М к стороне, а радиус вписанной окружности - перпендикуляр из точки О на плоскости трапеции к ее стороне. Основания этих перпендикуляров находятся в одной точке по теореме о трех перпендикулярах. Диаметр вписанной в нашу трапецию окружности пройдет через середины ее оснований, значит боковая сторона трапеции будет равна сумме двух отрезков: половин большего и меньшего оснований, так как касательные из одной точки к окружности равны, то АР=АН и ВР=ВN (см. рисунок). Но ОР - это высота из прямого угла треугольника АОВ (боковая сторона видна под углом 90° из центра вписанной окружности - свойство). и по ее свойству равна ОР = √(АР*ВР) = √(2*4,5) = 3 ед. Тогда по Пифагору из прямоугольного треугольника МОР найдем искомое расстояние МО.
МО=√(МР²-ОР²) = √(5²-3²) = 4 ед. Это ответ.
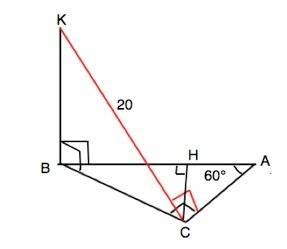
Сумма острых углов прямоугольного треугольника 90°⇒
∠АВС=90°-60°=30°
∆ ВСН прямоугольный, СН противолежит углу 30°.По свойству прямоугольного треугольника с углом 30° гипотенуза ВС = 2•СН=16 см
Расстояние от точки до прямой - длина отрезка, проведенного перпендикулярно к ней.
ВС⊥АС, ВС - проекция КС.
По т. о 3-х перпендикулярах КС⊥АС.⇒ КС - данное в условии расстояние от К до АС.
По условию ВК перпендикулярна плоскости АВС, следовательно, перпендикулярна любой прямой, проходящей через В. ⇒
∆ КВС прямоугольный,
По т.Пифагора КВ=√(KC²-BC²)=√(400-256)=12 см
Если AL=LB то треуг. ALB равнобедр., значит угол B=углу BAL=23, тогда угол А=46(AL биссектриса), угол С=180-23-46=111 гр.