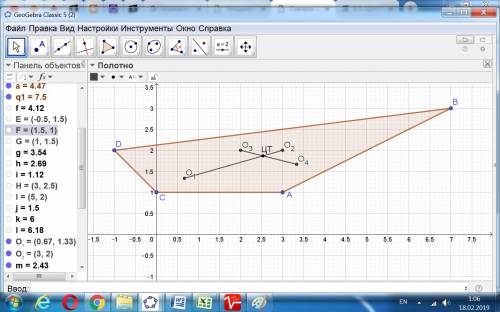
Сначала делим четырехугольник диагональю на два треугольника.
Находим центр тяжести каждого треугольника как точку пересечения его медиан. Центр тяжести четырехугольника лежит на прямой О1О2, соединяющей центры тяжести этих треугольников.
Затем делим четырёхугольник на 2 треугольника при другой диагонали и находим так же центры тяжести других треугольников. Соединяем их отрезком О3О4.
Искомый центр тяжести четырёхугольника лежит в точке ЦТ пересечения отрезков О1О2 и О3О4.
ABD x y BCD x y
O2 3 2 O3 2 2
ADC x y ABC x y
O1 0,6667 1,3333 O4 3,3333 1,6667
ЦТ = х у
2,533 1,8667
Объяснение:
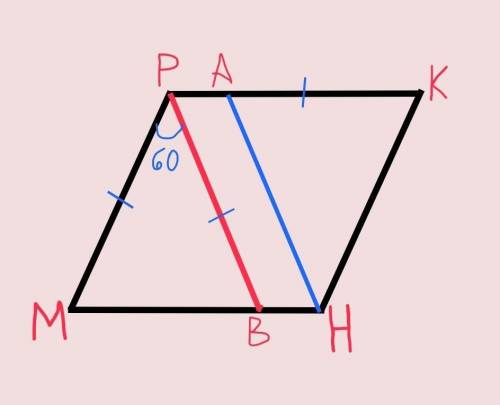
Так как МР=РВ по условию, то ∆МРВ – равнобедренный. Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.
Тогда угол PMB=угол РВМ=(180°–МРВ)÷2=(180°–60°)÷2=60°.
Получим что все углы ∆МРВ равны 60°, тогда ∆МРВ – равносторонний.
Тогда МВ=МР.
Углы при одной стороне параллелограмма в сумме равны 180°.
Значит угол МРК=180°–угол РМВ=180°–60°=120°
Противоположные углы параллелограмма равны.
Следовательно угол РКН=угол РМН=60°; угол МНК=угол МРК=120°.
МР=АК по условию
МР=КН так как противоположные стороны параллелограмма равны.
Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.
Следовательно: угол КАН=угол КНА=(180°–угол АКН)÷2=(180°–60°)÷2=60°.
Получим что все углы ∆АКН равны 60°, тогда ∆АКН – равносторонний. Исходя из этого АН=АК
МВ=МР=АК=АН => МВ=АН.
ответ: 1) 60°; 120; 2) равны.
Смотри. Задача не сложна если нарисовать рисунок.
Нам известна высота пирамиды и высота боковой грани. То есть это есть прямоугольной треугольник(высота пирамиды - перпендикуляр к основанию, а высота боковой грани - это гипотенуза. На рисунке чётко видно что треугольник DES - прямоугольный. Нам известна гипотенуза и катет, так давай найдём второй катет за теоремой Пифагора.
DE =
Разложим по формуле a²-b²=(a-b)(a+b)
DE =
=
- отрезок DE
Маленькая подсказка. Если с центра треугольника проведён отрезок к стороне треугольника тогда это радиус ВПИСАННОЙ окружности, а если к вершине - ОПИСАННОЙ
То есть DE - радиус вписанной окружности
Есть такая формула
r =
Где р - полупериметр, а S - площадь. Подставляем наши значения
12 = s/42
S = 12×42 = 504 см²