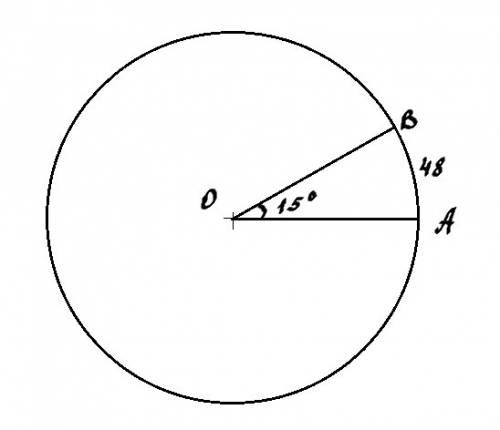
Угол АОВ центральный (смотри рисунок). Его градусная мера равна градусной мере дуги, на которую он опирается.
Малая дуга АВ равна 15°. Длина же ее равна 48.
Решим задачу, используя отношение.
Во сколько раз градусная мера большой дуги АВ больше градусной меры малой дуги АВ, во столько же раз длина большой дуги АВ больше длины малой дуги АВ.
Градусная мера всей окружности 360°.
360°–15° = 345° – градусная мера большой дуги АВ.
345°:15° = 23.
В 23 раза градусная мера большой дуги АВ больше градусной меры малой дуги АВ.
48*23 = 1104 – длина большой дуги АВ.
ответ: 1104.
Объяснение:
1. Если внутренние накрест лежащие углы равны, то прямые параллельны.
∠70°=∠70° ⇒
a║b
2. Если сумма внутренних односторонних углов равна 180, то то прямые параллельны.
∠110+∠70=180°⇒
c║d
3. Если соответственные углы равны, то прямые параллельны.
∠a=∠a
MD║|NK
4. Если соответственные углы равны, то прямые параллельны.
∠90=∠90
m║n
5. Если внутренние накрест лежащие углы равны, то прямые параллельны.
BC║AD
AB║CD
6. Если внутренние накрест лежащие углы равны, то прямые параллельны
∠EFL=∠FLK ⇒ EF║LK
∠EKF=∠KEL⇒ FK║EL
7. Если внутренние накрест лежащие углы равны, то прямые параллельны
∠NPM=∠PMQ ⇒NP║MQ
∠NMP=∠MPQ⇒NM║PQ
8. ΔAOB=ΔCOD (по двум сторонам и углу между ними)⇒
∠BAO=∠ODC если внутренние накрест лежащие углы равны, то прямые параллельны
AB║CD
9. ΔOXY=ΔOYZ по трем сторонам ⇒
∠XYO=∠YOZ ⇒ XY║OZ
∠XOY=∠OYZ⇒ OX║YZ
10.
UR║ST (внутренние накрест лежащие углы равны)
ΔRUO=ΔOST (по стороне и двум прилежащим к ней углам) ⇒
∠TRU=∠STR ⇒ RS║UT