Вариант для любителей тригонометрии
Объяснение:
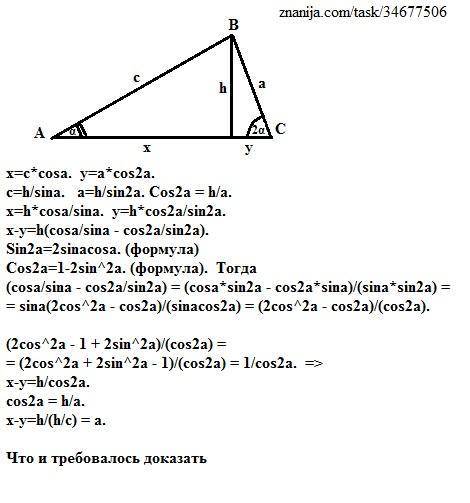
Дан треугольник АВС с основанием АС и высотой h, проведенной к основанию. Стороны треугольника
АВ = "с", ВС = "а".
Пусть основание делится высотой на отрезки, равные x и y, считая от вершины А. Тогда из прямоугольных треугольников, на которые высота делит исходный треугольник, имеем:
x = c*cosa. y = a*cos2a.
c = h/sina. a = h/sin2a. cos2a = h/а. =>
x = h*cosa/sina. y = h*cos2a/sin2a.
x - y = h(cosa/sina - cos2a/sin2a).
Sin2a = 2sina·cosa. (формула двойного аргумента)
Cos2a = 1 - 2sin²а. (формула двойного аргумента) Тогда
cosa/sina - cos2a/sin2a =
(cosa·sin2a - cos2a·sina)/(sina·sin2a). =>
sina(2cos²а - cos2a)/(sina·cos2a)=(2cos²а - cos2a)/(cos2a).
(2cos²а - 1 + 2sin²а)/(cos2a) =
(2cos²а + 2sin²а - 1)/(cos2a) = 1/cos2a. =>
x - y = h/cos2a. cos2a = h/а. =>
x - y = h/(h/а) = а.
Что и требовалось доказать.
средняя линия - полусумма оснований, значит две средние линии равны сумме оснований.
то есть нужно 48 (24*2) разбить на части, относящиеся как 2:3.
а это 2/5 и 3/5 от нее:
48*2/5 = 96/5 = 19,2
48*3/5 = 144/5 = 28,8
Второе тоже не сложно:
Снгова вспоминаем, что средняя линия - это среднее арифметическое, т.е. полусумма оснований. Значит, ее длина (5,6+2,4)/2 = 4м
несложный анализ картинки - трапеция со средней линией и диагональю - дает понимание, что диагональ делит среднюю линию пополам (нужно ли доказывать?)
Значит разбивает ее на отрезки по 2 метра
Ура!)