1) Из основного тригонометрического тождества найдем синус этого же угла
sin²α+cos²α=1
sinα=√1-cos²α
sinα=√1-0,64=√0,36=0,6
a/sinα=2R
R=a/(2sinα)
R=6/(2*0,6)=5 см
2) Высота проведенная к стороне равной 14 см делит ее на два отрезка. один отрезок обозначим х, а второй 14-х
Кроме того, высота (h) делит треугольник на два прямоугольных треугольника, в которых высота является катетом, а стороны равные 13 и 15 см гипотенузами. Воспользуемся теоремой пифагора для этих треугольников
а) h²=13²-x² для одного
б) h²=15²-(14-x)² для другого
так так высота одна и та же приравняем правые части выражений
169-х²=225-(196-28х+х²)
169-х²=29+28х-х²
169-29=28х
х=140/28=5 см часть стороны равной 14 см
воспользуемся формулой а) h²=169-25=144
h=12 см
3) Воспользуемся теоремой синусов и найдем угол С
АC/sinB=АВ/sinC
6√2/0,5=12/sinC
sinC=12/(12√2)=1/√2
Угол С=45°
Угол А=180-30-45=105°
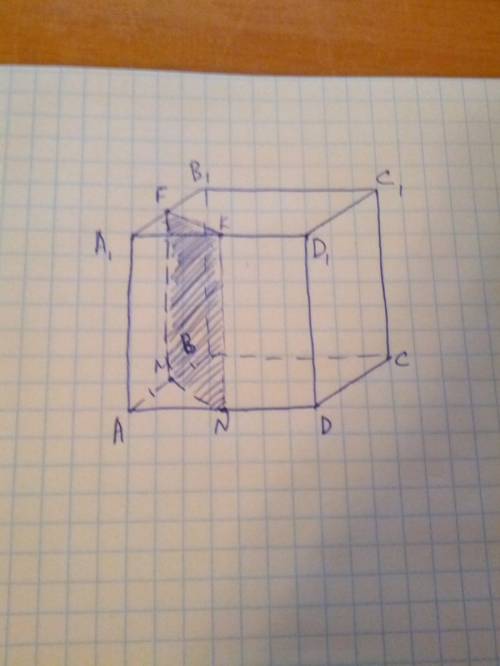
Построение сечения: Назовем искомую плоскость MNK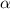 
. Плоскости ABC и A1B1C1 параллельны и пересечены плоскостью 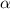, следовательно, линии пересечения параллельны. Значит, 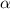пересекает А1В1С1 по прямой КF, параллельной MN. Значит, F - середина А1В1. Осталось соединить KF, FM, MN, NK. Искомое сечение - FKNM.
Доказательство: В треугольнике ABD MN-средняя линия, MN || BD. Т.к MN лежит в плоскости сечения MNK, а BD параллельна прямой MN, лежащей в плоскости сечения, ВD параллельна плоскости MNK, что и требовалось доказать.
Начнем.
8 задание.
1) Теорема: она лежащая против угла в 30 градусов равна половине гипотенузы.
По этой теореме находим, что АС=24см.
2) По теореме Пифагора: АС=CD+AD
Получается AD=12√3 см.
3) Проводим перпендикуляр BK. Так как это прямоугольная трапеция, то угол d=90, c=90, и проведя перпендикуляр образовались тоже прямые углы, значит KBCD квадрат, тем самым делаем вывод, что BK=12cm, KD=12cm., BC=12 cm.
И спокойно находим площадь.
S=(a+b)*h:2
Получаем ответ S=144√3cm.