1. Периметр правильного треугольника описанного около окружности равен 18 см. Найти площадь правильного шестиугольника вписанного в эту окружность.
2. Диагональ МК параллелограмма МЕКD равна 18 см. Середина A стороны ME соединена с вершиной D. Найдите отрезки, на которые делится диагональ MK отрезком DA.
3. Дана окружность радиуса 6 см. Найти площадь сектора, соответствующего дуге длиной 6см.
Назовём данный треугольник АВС.
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=30:2=15 см
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см
Высоты к боковым сторонам найдем из площади ∆ АВС
Заметим, что ∆ АВС - тупоугольный ( АС² > АВ²+ВС²), поэтому высоты, проведенные к боковым сторонам тупоугольного треугольника, лежат вне его.
S(ABC)=BB1•AC:2=8•15=120 см²
AA1=2S(ABC):BC
AA1=CC1=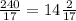 см
см