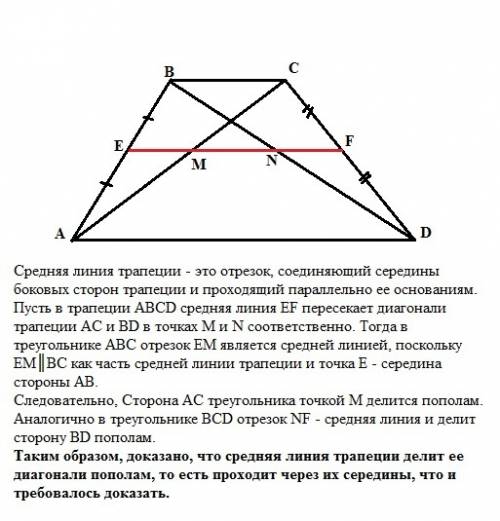
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон трапеции и проходящий параллельно ее основаниям.
Пусть в трапеции АВСD средняя линия EF пересекает диагонали трапеции АС и ВD в точках М и N соответственно. Тогда в треугольнике АВС отрезок ЕМ является средней линией, поскольку ЕМ║ВС как часть средней линии трапеции и точка Е - середина стороны АВ.
Следовательно, Сторона АС треугольника точкой М делится пополам.
Аналогично в треугольнике ВCD отрезок NF - средняя линия и делит сторону BD пополам.
Таким образом, доказано, что средняя линия трапеции делит ее диагонали пополам, то есть проходит через их середины, что и требовалось доказать.
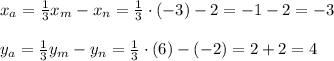
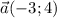
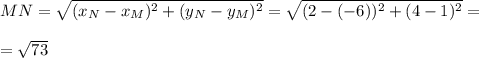
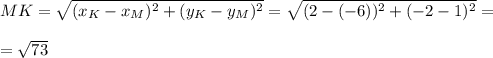
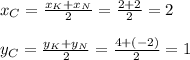
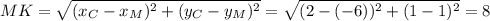

Пусть СА - касательная, где т.С ∉ окружности; т.А и т.В ∈ окружности.
∠ВАС - угол между касательной АС и хордой АВ
∠ВАС=1/2 ∪ АВ (дуги АВ) ⇒
∪АВ=58*2=116°
∠АОВ=116° (центральный угол = ∪, на которую опирается.
Рассм. ΔАОВ; он равнобедренный ⇒
∠АВО=∠ВАО (углы при основании р/б Δ)
∠АВО=(180-116):2=32° - это ответ.