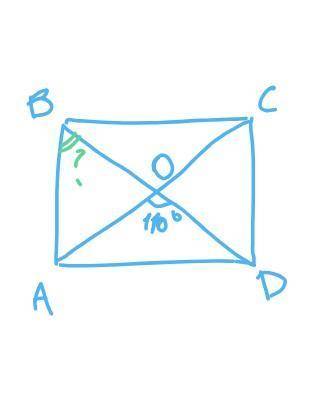
Диагонали прямоугольника имеют одинаковую длину, AC = BD;
Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам,
AO = OC = BO = OD;
Получается, треугольник ABO — равнобедренный (BO = AO), углы при основании равнобедренного треугольника равны, ∠ABO = ∠OAB;
∠ABD — это тот же ∠ABO;
∠AOB + ∠AOD = 180° (лежат на одном развёрнутом угле BOD), ∠AOB = 180° – ∠AOD = 180° – 110° = 70°;
Сумма углов треугольника равна 180°,
∠ABO + ∠AOB + ∠OAB = 180°,
Подставляем, что ∠ABO = ∠OAB, получаем
2 × ∠ABO + ∠AOB = 180°,
2 × ∠ABO = 180° – ∠AOB = 180° – 70° = 110°,
∠ABO = 110° ÷ 2 = 55° = ∠OAB
ответ: 55°
В треугольнике АСВ медиана СН разделила его на два треугольника.
=>Высоты треугольников СВН и САН равны (НЕ=НМ), а основания равны (АС=СВ)
И площадь каждого из этих треугольников равна половине площади треугольника АСВ.
Площадь прямоугольного треугольника равна половине произведения его катетов.
Точно так же медиана ВО треугольника ВСН делит его на два равновеликих треугольника с одинаковой высотой, и площадь каждого равна половине площади треугольника ВСН.
И,соответственно,одной четвертой площади треугольника АВС.
ответ: