1)
A(6,0)
B(0,8)
(3,4)
10
2)
O(3,7)
(x-3)^2+(y-7)^2=65
y=2x-5
Объяснение:
1) Если прямая пересекается с осью ox, то координата y точки пересечения равна 0. Подставляем это значение в уравнение прямой и, решая его, находим координату x точки пресечения.
(вычисления на скрине 1)
A(6,0)
B(0,8)
Координаты середины отрезка вычисляются по формуле (скрин 2)
Длина отрезка вычисляется по формуле (скрин 3)
2) Если прямые пересекаются, то координаты точки пересечения удовлетворяю каждому уравнению. Приравняем и решим относительно x, а потом подставим значение в любое уравнение (скрин 4)
Найдем радиус окружности (расстояние от O до B) и запишем уравнение окружности (скрин 5.1)
Параллельность = равенство угловых коэффициентов. Исходя из этого найдем b и запишем уравнение (скрин 5.2)
ꟷꟷꟷꟷꟷꟷ
Не забывайте сказать " "! и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!
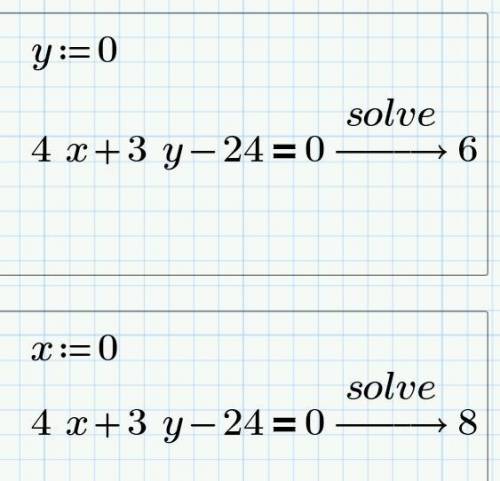
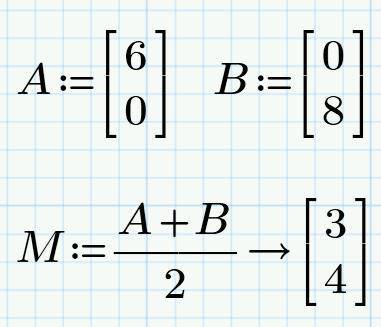
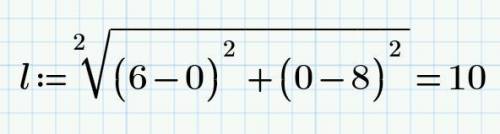
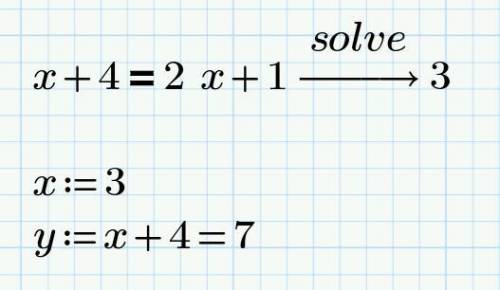
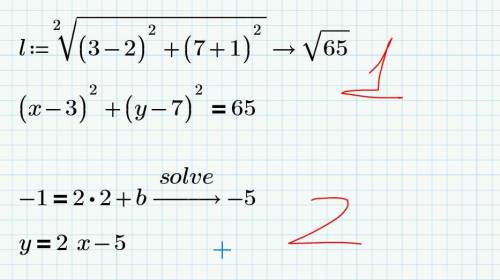
1) Смежные углы в сумме дают 180°. Один 28°, другой 152°
2) При пересечении двух прямых получаются 2 вертикальных угла
(равны друг другу) и два смежных (в сумме 180°).
Углы равны 70°, 70°, 110°, 110°.
3) Если внешний угол равен 40°, то внутренний 180° - 40° = 140°.
Второй угол равен 30°, а третий 180° - 140° - 30° = 10°
4) В равнобедренном треугольнике медиана - она же биссектриса и высота.
Поэтому боковые стороны AB=BC, сторона BO общая, углы ABO=CBO.
По 2 признаку равенства треугольников (2 стороны и угол) эти треугольники равны.
5) Углы прямоугольного треугольника A = 90°, C = 15°, B = 75°.
Угол В делят на CBD = 15° и ABD = 60°.
Значит, угол ADB = 90° - 60° = 30°. Катет против угла 30° равен половине гипотенузы.
а) Значит, гипотенуза BD = AB*2 = 3*2 = 6 см.
б) Треугольник BDC - равнобедренный с углами B = C = 15°, D = 150°.
Стороны BD = DC = 6 см.
По правилу треугольника, сторона BC должна быть меньше суммы двух других сторон.
BC < BD + DC = 6 + 6 = 12 см.