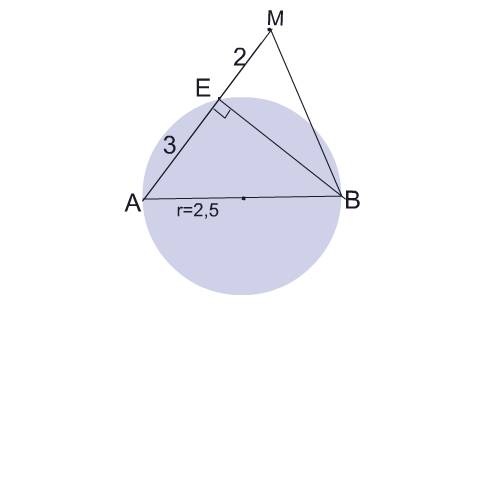
Cоедини конец диаметра В с точкой Е.
Получишь прямоугольный треугольник АВЕ, т.к. вписанный треугольник,одна из сторон которого - диаметр, является прямоугольным.
ВЕ - высота треугольника АМВ, в то же время катет прямоугольного треугольника АВЕ.
Можно ВЕ определить по теореме Пифагора, можно просто вспомнить, что третья сторона этого египетского треугольника равна 4, т.к. две других - 3 и 5, и второй катет прямоугольного треугольника с гипотенузой 5 и катетом 3 всегда равен 4.
Итак, имеем высоту треугольника АМВ, равную 4 см, имеем основание этого треугольника
АМ=2+3=5 см
Площадь тр-ка АМВ находится по классической формуле
S=½ h·a
S=4·5:2=10 cм²
Угол правильного шестиугольника при вершине раравен 120 гр.
Периметр правильного треугольника, вписанного в окружность, равен 45 см. Следовательно сторона треугольника равна 15 см. По условию задачи каждой стороне треугольника соответствует две стороны шестиугольника. Вследствии чего нужно просто решить задачку с равнобедренным треугольником, основание которого 15 см, а угол вершины 120 гр. У таког треугольника углы при основнии равны (180-120)/2=30 гр. Опускаем высоту из угла 120 гр, получаем прямоугольный треугольник с углами
90; 60; 30 гр. Далее сos (30°) = cos (π/6) = (√3)/2, следовательно сторона шестиугольника, обозначим её как А=7,5*сos (30°)=7,5*(√3)/2 см.
А=7,5*(√3)/2=(15/4)*√3 см.