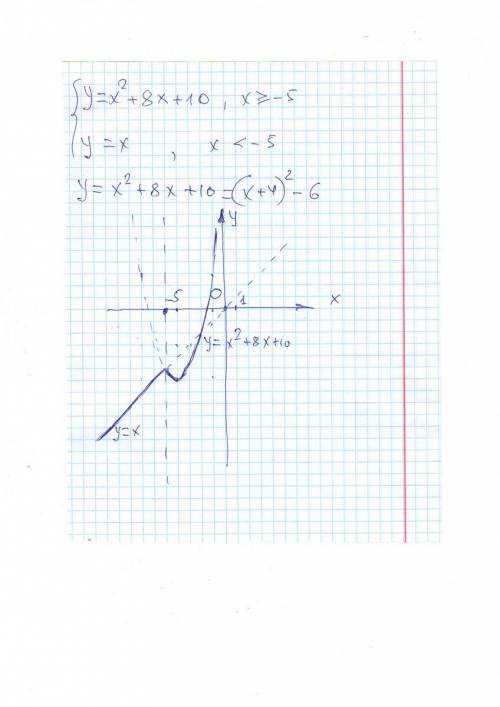

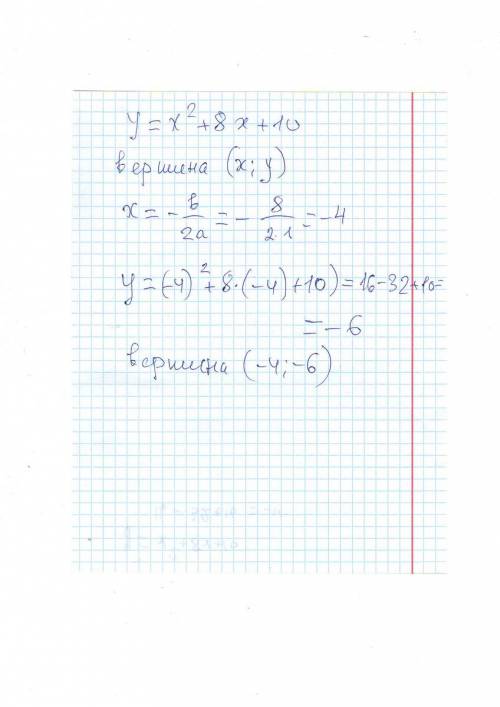
Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру
r=S:p
Ни площади, ни полупериметра мы пока не знаем, но можем узнать.
Поскольку отрезок, соединяющий центр гипотенузы с противоположным катетом перпендикулярен к нему, он от начального треугольника отрезает подобный ему.
Коэффициент подобия этих треугольников 2, так как гипотенуза вдвое больше своей половины.
Следовательно, второй катет большего треугольника равен
2,5*2=5 см
Гипотренуза равна
√ (144+25)=13 см
Площадь треугольника
12*5:2=30 см²
полупериметр
12+5+13=30 см
30:2=15 см
r=S:p=30:15=2 см
По свойствам касательных к окружности мы знаем, что АВ=ВС. Посмотрим на треуг. АВС: он равнобедренный и прямоугольный, значит АК - высота и бессиктриса => ∠ВАК=∠САК=45 градусов.
Рассмотрим треуг. АСО: угол С=90 градусов(т.к. радиус перпендикулярен касательной), угол СОА=180-90-45=45 градусов, значит, треугольник АСО - равнобедренный и АС=СО, а СО=ВО=R.
Рассмотрим четырехугольник АВОС: все стороны равны, ∠А=90 градусов, ∠В=90 градусов, ∠С=90 градусов, значит ∠О=90 градусов => АВОС-квадрат => АО=ВС=10 см.
Вуаля;) Прикрепила картинку из интернета и нарисовала свою, чтобы понятнее было))) Удачи)
ответ: 10 см.