1. Треугольник АВС вписан в окружность радиуса 3√3 см.Найдите АВ, если
∠А=50˚, ∠В=70˚.
2. Найдите сторону треугольника, лежащую против угла 45˚, если две другие стороны равны √2 и 4.

👇

Открыть все ответы

Ответ:

Макси00084322233

14.02.2023

Пусть О - точка пересечения медиан треугольника АВС. Треугольники AOP и BOM подобны по двум углам (два угла равны по условию, еще два угла вертикальные). Тогда:
$\frac{AO}{OB} = \frac{PO}{OM}$
Так как медианы точкой пересечения делятся в отношении 2:1, то:
$\frac{ \frac{2}{3} AM}{ \frac{2}{3} BP} = \frac{\frac{1}{3}BP}{\frac{1}{3}AM}
\\\
\frac{ AM}{ BP} = \frac{BP}{AM}
\\\
AM^2=BP^2
\\\
\Rightarrow AM=BP=1$
Если медианы, проведенные к двум сторонам треугольника равны, то и сами стороны также равны. Значит, АС=ВС и треугольник АВС равнобедренный.
Рассмотрим треугольник АМС. По теореме косинусов, учитывая соотношение АС=2СМ, получим:
$AM^2=AC^2+CM^2-2\cdot AC\cdot CM\cdot\cos ACB
\\\
1^2=(2CM)^2+CM^2-2\cdot 2CM\cdot CM\cdot0.8
\\\
1=4CM^2+CM^2-3.2CM^2
\\\
1=1.8CM^2
\\\
CM^2= \frac{1}{1.8} = \frac{5}{9} 
\\\
CM= \frac{ \sqrt{5} }{3}$
Следовательно стороны в два раза больше: $AC=BC= \frac{2 \sqrt{5} }{3}$
Тогда площадь треугольника найдем как половину произведения двух его сторон на синус угла между ними:
$S= \frac{1}{2} \cdot AC\cdot BC\cdot \sinACB
\\\
S= \frac{1}{2} \cdot AC^2\cdot \sqrt{1-\cos ACB} 
\\\
S= \frac{1}{2} \cdot ( \frac{2 \sqrt{5} }{3})^2\cdot \sqrt{1-0.8}=\frac{1}{2} \cdot \frac{4\cdot5 }{9} \cdot \frac{3}{5} = \frac{2}{3}$
ответ: 2/3

4,4(4 оценок)

Ответ:

andreyoy

14.02.2023

Р = 80 см.

Объяснение:

Пусть трапеция ABCD и АВ = CD.

Середина большего основания - точка М.

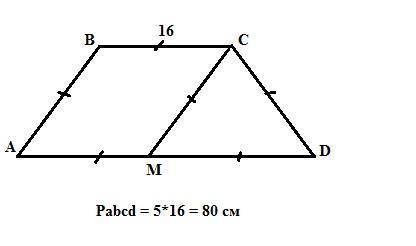
Расстояние от середины большего основания до вершины тупого угла равно меньшему основанию, а большее основание в 2 раза больше меньшего основания. Следовательно, соединив середину большего основания М с вершиной тупого угла С, получим параллелограмм АВСМ, так как противоположные стороны ВС и АМ параллельны и равны, а это признак параллелограмма. Кроме того, Стороны СМ, ВС и АМ равны, следовательно, ABCD - ромб. Кроме того, АВ = CD (дано). Итак,

АВ=ВС=CD = 16см, а AD = 32см. Значит периметр трапеции равен

АВ+ВС+CD+AD = 3*16+32 = 80см.