Ритмичность — это периодическая повторяемость каких-либо явлений и процессов во времени. Ритмичность характерна и для географической оболочки. Ритмы есть как в живой, так и в неживой природе. Однако в живой природе они сформировались вследствие ритмов неживой природы.
Ритмичность — это периодическая повторяемость каких-либо явлений и процессов во времени. Ритмичность характерна и для географической оболочки. Ритмы есть как в живой, так и в неживой природе. Однако в живой природе они сформировались вследствие ритмов неживой природы.
Целостность географической оболочки проявляется в том, что изменение одного компонента природного комплекса неизбежно вызывает изменение всех остальных и всей системы, как целого. К тому же, изменения, произошедшие в одном месте, отражаются на всей оболочке, а иногда на какой-либо ее части – в другом месте.
Зональность – это закономерное изменение природных компонентов и природных комплексов по направлению от экватора к полюсам. Зональность обусловлена неодинаковым количеством поступающего на разные широты тепла в связи с шарообразной формой Земли. Зональны климат, растительность, почвы, животный мир.
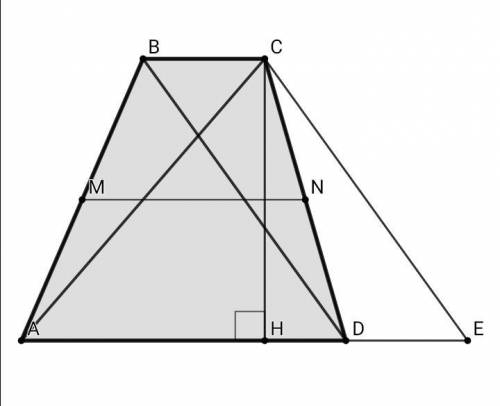
Выведу обобщённую формулу для подобных задач про трапецию с известными диагоналями AC = x, BD = y, и суммой оснований BC + AD = m
Проведём из вершинны С прямую СЕ, параллельную BD, тогда BC || DE, CE || BD ⇒ BCED - параллелограми, ВС = DE, CE = BD = y
S (abcd) = (BC + AD)•CH/2 = (DE + AD)•CH/2 = AE•CH/2 = S (ace)
Площадь трапеции ABCD равна площади треугольника ACE
Найдём плошадь ΔАСЕ по формуле Герона: АС = х, CE = y, AE = m
Площадь трапеции с диагоналями х и у и суммой оснований равной m:S = √( p • (p - x) • (p - y) • (p - m) ) , где р = (х + y + m)/2Средняя линия трапеции: MN = (BC + AD)/2 = 5 ⇒ m = 10, x = 9, у = 17
S (abcd) = √(18•(18 - 9)(18 - 17)(18 - 10)) = √(18•9•1•8) = 36ответ: 36
ответ:«Серед рівних розумом - за однакових умов –
переважає той, хто знає геометрію»
Блез Паскаль
Центром вписаного у трикутник кола є точка перетину
його бісектрис. Центр вписаного кола знаходиться всередині
трикутника.
Центром описаного навколо трикутника кола є точка перетину серединних перпендикулярів, проведених
до його сторін.
Гострокутний трикутник
Прямокутний трикутник Тупокутний трикутник
R
r
a
Варіант 29. Завдання 2.6
Як відноситься сторона правильного трикутника,
вписаного в коло, до сторони правильного трикутника,
описаного навколо цього кола?
Для АВС коло є вписаним,
а для MNK коло є описаним
NM : АВ = 1 : 2
R=2r
Для рівностороннього трикутника
Объяснение: