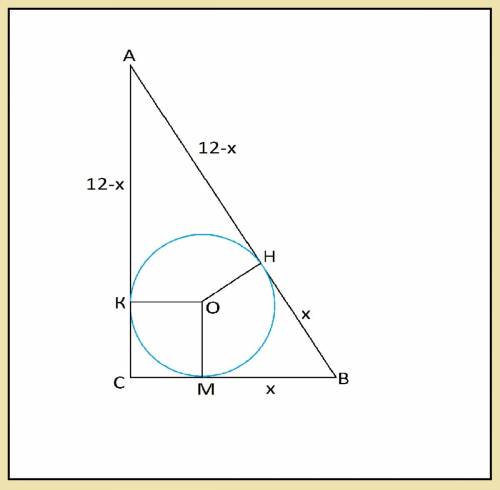
4. Окружность, вписанная в треугольник ABC, касается сторон AB, BC и AC в точках K, рим соответственно. - id1306449620200929 от dasa2208 29.09.2020 18:02

Question

Геометрия: 4. Окружность, вписанная в треугольник ABC, касается сторон AB, BC и AC в точках K, рим соответственно. Найдите длину отрезка MA, если CB=10 см и РДАВС = 24. см. 5. Постройте равнобедренный треугольник по углу, противолежащему основанию, и высоте, проведённой к основанию. (Подсказка: в дано вы должны начертить один отрезок и один угол. Используйте свойство равнобедренного треугольника.)​

dasa2208 · Accepted Answer

Нарисуем треугольник АВС ( С=90°) и вписанную в него окружность.
Из центра в точки касания проведем радиусы, которые, как известно, перпендикулярны касательным в точках касания.
Обозначим точки касания К на АС, М - на СБ, и Н на АВ.
По свойству отрезков касательных
АК=АН, МВ=ВН, и КС=СМ=r=2
Пусть МВ=х
Тогда ВН=х, а АК=АН=12-х
АС=12-х+2=14-х
ВС=х+2
По т.Пифагора АС²+ВС²=АВ²
(14-х)²+(2+х)²=144⇒
x² - 12*x + 28 = 0
D=32
х₁=(12+ 2√8):2=6 + √8
х₂=6-√8
ВС=6 + √8+2=8+√8
АС=14-(6 + √8)=8-√8
S (АВС)=АС*ВС:2=(8+√8)(8-√8)
S (АВС)=(64-8):2=28 (единиц площади)
---
Площадь будет такой же, если используем второе значение х₂=6-√8
Втреугольнике авс угол с равен 90 градусов. радиус вписанной окружности равен 2. найдите площадь тре

Втреугольнике авс угол с равен 90 градусов. радиус вписанной окружности равен 2. найдите площадь тре

MOGZ ответил