1).
Обозначим искомую сторону с
По теореме косинусов
с²=а²+b²- 2ab(cos(C)
с²=32+36 - 24√2·(135°)
Косинус тупого угла - величина отрицательная.
с²=32+36 - 24√2·(- 0.7071)
с²=68+ 24 · 0,999990=92
c=√92 см
c=2√23 см
-------------------------------
2).
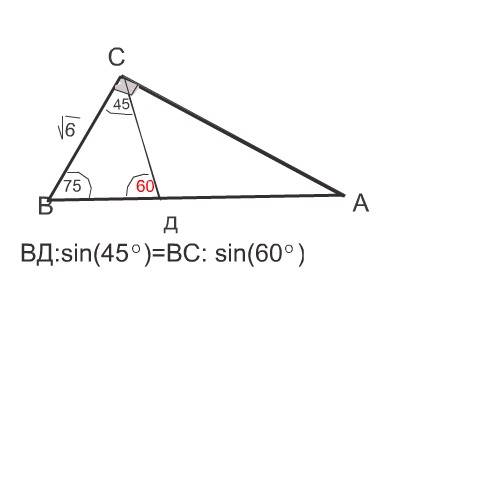
ВД:(√2:2)=√6:(√3):2)
(√2:2)·√6= ВД·(√3):2)
√2 ·√6= ВД·√3
√12 = ВД·√3
2√3=ВД·√3
ВД=2
-----------------------------------
3).
Проведем ВН ⊥АД
ВН=НД как катеты равнобедренного ⊿ ВНД с углами при ВД=45°
ВД=ВН·√2
6√3 =ВН ·√2
ВН=6√3:√2
умножим числитель и знаменатель дроби 6√3:√2 на √2
ВН=6√3:√2=6√3·√2:√2·√2=3√6
sin BAH=ВН:АВ
sin BAH=3√6:6√2=√3·√2:2√2=√3:2
√3:2=sin (60°)
∠ВАД=60°
-----------
∠ВАД=∠ВСД=60°
∠АВС=∠СДА=120°
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.
Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.
Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.
Свойства правильного многоугольника.
* Правильный многоугольник является вписанным в окружность и описанным около окружности, при этом центры этих окружностей совпадают
* Центр правильного многоугольника совпадает с центрами вписанной и описанной окружностей.
* Сторона an правильного n-угольника связана с радиусом R описанной окружности формулой an=2Rsinn180=2Rsinn.
* Периметры правильных n-угольников относятся как радиусы описанных окружностей.
это точные определения которые пригодятся в решении