Условие не совсем корректное. В равностороннем треугольнике нет большей или меньшей стороны, на то он и равносторонний.
В сети можно найти несколько вариантов похожих задач с разными данными.
Вариант 1.
Решаем задачу о равнобедренном треугольнике АВС (АВ=ВС) с боковой стороной, равной 4, и большей стороной АС.
АС=0,75•(4+4)=6 см
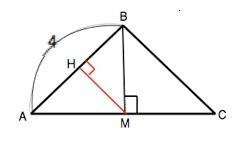
Биссектриса угла против основания равнобедренного треугольника совпадает с высотой и медианой, поэтому АМ=СМ и ∆ АВМ=∆ СВМ – прямоугольные.
Искомое расстояние - высота МН треугольника АВМ.
cos BAM=AM:AB=3/4
MH=AM•sin HAM
sin(HAM)=√(1-cos*)=√(1- 9/16)=√7/4
MH=3√7/4
——
Возможно, задача все же о разностороннем треугольнике.
Вариант 2.
В разностороннем треугольнике большая сторона составляет 75% суммы двух других. Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см.
Здесь условие корректное - есть и большая сторона, и меньшая.
АС=0,75•(AB+BC)
По свойству биссектрисы треугольника ВМ делит противоположную углу сторону АС в отношении прилежащих сторон.
АВ:ВС=АМ:СМ
АМ=0,75 АВ
Меньшая высота - высота, проведена к большей стороне. ВК=4
Из формулы площади треугольника
ВК•AM=MH•AB
НМ=ВК•AM:AB ⇒ НМ=ВК•0,75 АВ:AB
HM=4•0,75=3 см
d=a*корень(3)
V=a^3
1) корень(8):корень(3)=2корень(2/3) - ребро куба
(2корень(2/3))^3=8*2/3*корень(2/3)=16/3*корень(2/3) - обьем куба
2) обьем куба пропорционален кубу ребра, поєтому при увеличении ребра в три раза обьем увеличится в 3*3*3=27 раз