Sосн=36см²
Sбок=224см²
Sпол=296см²
V=288cм³
Объяснение:
Дано
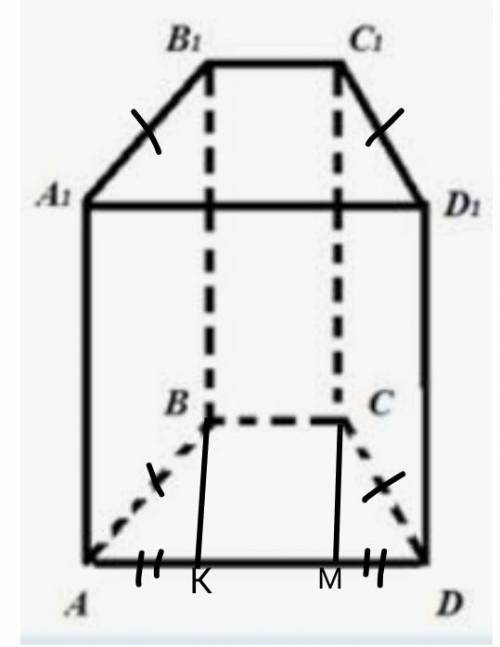
ABCDA1B1C1D1- призма
ABCD- трапеция
АВ=CD=5см боковая сторона трапеции.
ВС=6см верхнее основание трапеции.
АD=12см нижнее основание трапеции.
В1В:ВК=2:1.
Sосн.=?
Sбок=?
Sпол=?
V=?
Решение.
АК=МD
AK=(AD-BC)/2=(12-6)/2=6/2=3 см.
∆АВК- прямоугольный (<ВКА=90°)
По теореме Пифагора найдем высоту трапеции.
ВК²=АВ²-АК²=5²-3²=25-9=16см.
ВК=√16=4 см высота трапеции.
Sосн=ВК(ВС+AD)/2=4*(6+12)/2=4*18/2=
=36см² площадь трапеции.
ВВ1=2*ВК=2*4=8см высота призмы.
Росн=АВ*2+ВС+AD=5*2+6+12=10+18=28см периметр трапеции.
Sбок=Росн*ВВ1=28*8=224см² площадь боковой поверхности призмы.
Sпол=2Sосн+Sбок=2*36+224=72+224=
=296 см² площадь полной поверхности призмы.
V=Sосн*ВВ1=36*8=288см³ объем призмы.
ответ. 102.
Объяснение:
Решение. Проведем отрезки BD и CE. Пусть они пересекаются в точке О. Заметим, что треугольники BCD и CDE равнобедренные с углом 108 при вершине, а значит, углы при основании равны 36 (они отмечены на рисунке одной дугой). Тогда BCE = BDE = 72. Угол COD равен 108 (т.к. в треугольнике COD два угла по 36). Поэтому COB = 180108 = 72. Углы по 72 отмечены на рисунке двумя дугами. Получаем, что треугольники CBO и DEO равнобедренные. Значит, AB = BO =BC = CD = DE = EO = х. Заметим, что OBA = 9636 = 60. Значит, треугольник OBA равнобедренный с углом 60 при вершине, т.е. равносторонний. Поэтому AO = x. Вычислим угол AOE AOE = EOBAOB = 10860 = 48. Треугольник AOE равнобедренный с углом 48 при вершине. Поэтому OEA = (18048)/2 = 66. Получаем, что угол E пятиугольника равен AED = AEO+OED = 66+36 = 10
A=40,B=60,C=80
Объяснение:
потомучто