Если двугранные углы при ребрах основания равны (равны углы наклона боковых граней к плоскости основания), то высота пирамиды проецируется в центр окружности, вписанной в основание. В ромбе это точка пересечения диагоналей (точка О на рисунке).
Проведем ОН⊥CD. ОН - проекция наклонной SH на плоскость основания, тогда SH⊥CD по теореме о трех перпендикулярах. Значит
∠SHO = 60° - линейный угол двугранного угла при ребре основания.
Периметр ромба 40 см, значит длина одной стороны ромба
CD = Pabcd/4 = 10 см.
КН - высота ромба.
Sabcd = CD · KH
KH = Sabcd / CD = 60 / 10 = 6 см
ОН = 1/2 КН = 3 см.
ΔSOH: ∠SOH = 90°,
SO = OH · tg∠SOH = 3 · √3 = 3√3 см
Объем пирамиды:
V = 1/3 Sabcd · SO = 1/3 · 60 · 3√3 = 60√3 см³
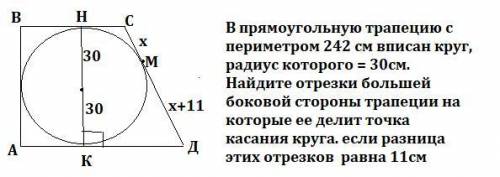
В прямоугольную трапецию с периметром 242 см вписан круг, радиус которого = 30см. Найдите отрезки большей боковой стороны трапеции на которые ее делит точка касания круга. если разница этих отрезков равна 11см
Объяснение:
Большая боковая сторона это СД
Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны⇒АВ+СД=ВС+АД=242:2=121 (см).
Радиус, проведенный в точку касания перпендикулярен касательной ⇒ R=НК=АВ=30*2=60(см).
Значит АВ+СД=121 , 60+СД=121 , СД=61 см.
Пусть меньший отрезок стороны СД будет х см, тогда больший отрезок стороны СД= будет х+11, а из сумма 61 см. Составим уравнение : х+х+11=61 , х=25см
Меньший отрезок 25 см, больший отрезок 25+11=36 (см)
Объяснение:
Площадь трапеции
S=\frac{1}{2}*(a+b)*h
Пусть а - меньшее основание, а b - большее. Тогда, по условию задачи
a=3h, b=5h
S=\frac{1}{2}*(3h+5h)*h=\frac{1}{2}*8h^{2}=4h^{2}
4h^{2}=100
h^{2}=25
h=5
a=15
b=25