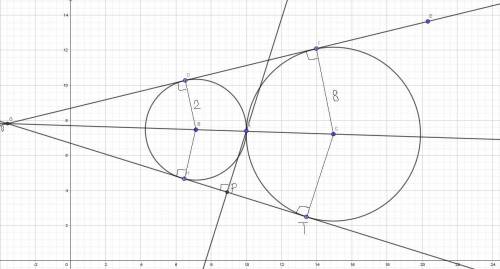
Рисунок прилагается. Таких внешних касательных существует всего две. Они пересекаются в точке G. BD и CF - радиусы, перпендикулярные касательной GE. Треугольники GDB и GFC подобны по двум углам (G - общий угол, а также ∠GBD=∠GFC=90° (как раз эти самые радиусы)
Тогда из подобия 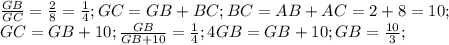
Наше искомое расстояние AP. Это заодно значит, что AP перпендикулярно GT (второй касательной, можно было так же начертить и с первой, это не принципиально). Тогда треугольники GBH и GAP тоже подобны по двум углам (G - общий и ∠GHB=∠GPA=90°)
и значит, что 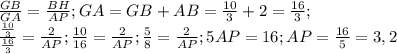
ответ: 3,2 см.
ответ: S=336см²
Объяснение: обозначим вершины ромба А В С Д, а диагонали АС и ВД, точку их пересечения О. Диагонали пересекаясь делят ромб на 2 равных прямоугольных треугольника в которых его диагонали являются катетами а стороны - гипотенузой. Пусть диагональ ВД=х, а вторая АС=у. Если их сумма составляет 62см, то х+у=62
Если рассмотреть =АВО, тодиагонали при пересечении делятся пополам поэтому
ВО=ДО=х/2, АО=СО=у/2. Составим уравнение используя теорему Пифагора:
(х/2)²+(у/2)²=25². У нас получилась система уравнений:
х+у=62
(х/2)²+(у/2)²=25²
х=62-у
Подставим значение х во второе уравнение: (х/2)²+(у/2)²=25
((62-у)/2)²+у²/4=625
(62-у²)/4+у²/4=625
(3844-124у+у²+у²)/4=625
(2у²-124у+3844)/4=625
2у²-124у+3844=4×625
2у²+124у+3844=2500
2у²+124у+3844-2500=0
2у²+124у+1344=0 |÷2
у²-62у+672=0
Д=3844-4×672=3844-2688=1156
у1=(62-34)/2=28/2=14
у2=(62+34)/2=96/2=48
Итак: у1=14; у2=48
Теперь подставим значение у в первое уравнение: х1=62-у=62-14=48
х2=62-48=14
Нам подходят оба значения х и у. Диагональ ВД=48см; АС=14см
Площадь ромба можно вычислить по формуле S=½×AC×BД=½×14×48=336см²