Мера двугранного угла равна 60°.
Объяснение:
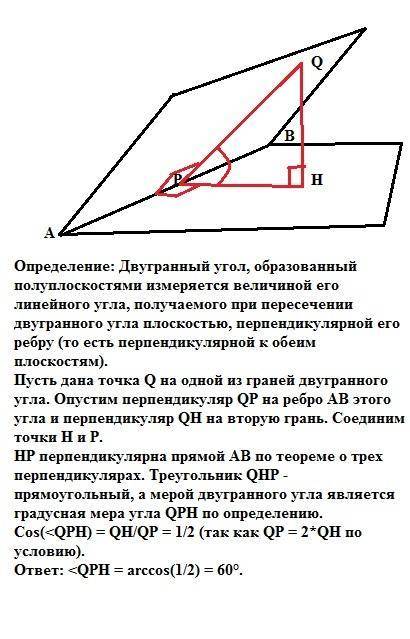
Определение: Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям).
Пусть дана точка Q на одной из граней двугранного угла. Опустим перпендикуляр QР на ребро АВ этого угла и перпендикуляр QH на вторую грань. Соединим точки Н и Р.
НР перпендикулярна прямой АВ по теореме о трех перпендикулярах. Треугольник QHP - прямоугольный, а мерой двугранного угла является градусная мера угла QPH по определению. Косинус этого угла равен отношению прилежащего катета к гипотенузе, то есть Cos(<QPH) = QH/QP = 1/2 (так как QP = 2*QH по условию).
ответ: <QPH = arccos(1/2) = 60°.
Объяснение:
1)
Рисунок а.
Проведём две высоты ВМ и СК.
ВМ=АМ, так как ∆АВМ- прямоугольный, равнобедренный
cos45°=AM/AB
√2/2=AM/8
AM=8√2/2=4√2 см.
ВМ=4√2 см.
СК=ВМ=4√2 см.
∆СКD- прямоугольный треугольник.
СD- гипотенуза.
СК и KD- катеты
По теореме Пифагора найдем
КD²=CD²-CK²=6²-(4√2)²=36-32=4см
КD=√4=2 см.
МК=AD-AM-KD=16-4√2-2=14-4√2 см.
МК=ВС=14-4√2см.
S(ABCD)=BM*(BC+AD)/2=4√2(16+14-4√2)/2=
=2√2(30-4√2)=60√2-16 см².
ответ: 60√2-16см²
2) Рисунок б
Проведём высоту СК.
cos30°=KD/CD
√3/2=KD/8
KD=8√3/2=4√3 см
sin30°=CK/CD
1/2=CK/8
CK=8/2=4см высота трапеции.
BC=AD-KD=6√3-4√3=2√3 см.
S(ABCD)=CK(BC+AD)/2=4*(2√3+6√3)/2=
=2*8√3=16√3 см²
ответ: 16√3см²