Правильная 4-я пирамида - в основании квадрат, боковые ребра равны. Пирамида усечена параллельно основанию. Диагональное сечение данной фигуры - равнобедренная трапеция.
Высота правильной пирамиды проецируется в центр описанной окружности основания. Центр описанной окружности квадрата - пересечение диагоналей. Диагональное сечение проходит через вершину и диагональ основания, следовательно высота лежит в плоскости сечения. Достаточно найти высоту сечения.
В сантиметрах
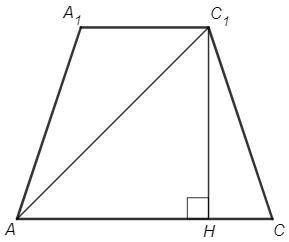
Рассмотрим трапецию AA1C1C.
A1C1 =A1B1 √2 =4√2 (диагональ квадрата)
AC =AB √2 = 8√2
Опустим высоту C1H.
AH =(AC +A1C1)/2 =6√2
C1H =√(AC1^2 -AH^2) =√(144-72) =6√2 (см)
1.Тень от фонарного столба будет 4+8=12м, то есть в 12/4=3 раза больше, чем тень от дерева. Значит и высота столба будет в 3 раза больше дерева, то есть 3*3=9м.
2.Треугольник АВС - прямоугольный.
Докажем это с применением теоремы Пифагора:
41²=40²+9²
1681=1600+81
Значит, АС - гипотенуза.
В прямоугольном треугольнике центр окружности находится посередине гипотенузы, следовательно, радиус окружности равен 41:2=20,5 см.
ответ: 20,5 см
3.(картинка)
4.Опустим из вершины равнобедренного треугольника высоту, которая по известной теореме является медианой и биссектрисой. Тогда из получившихся прямоугольных треугольников найдем, что
sin(α/2) = (x/2)/b = x/(2b), где x - это длина искомого основания. Теперь выразим икс.
x = 2b*sin(α/2).
5.Опускаем перпендикуляр BD на сторону AC.
Проекция AB на AC - это AD= AB cos A; проекция BC на AC - это CD= BC cos C.(Картинка 2)Из теоремы синусов
Объяснение: