Пусть основание АВ, вершина, из которой проведены медиана и высота - С, середину АВ обозначим М, основание высоты К (СК - высота к АВ). Опишем вокруг АВС окружность и продлим СМ и СК до пересечения с ней. Пусть это точки, соответственно Е для СМ и Р для СК.
Мы знаем, что дуги АЕ и ВР равны.
Поэтому ЕР II AB
=> ЕР перпендикулярно СР,
=> EC - диаметр,
и => М - центр окружности. В самом деле, АМ = МВ, но АВ не перпендикулярно ЕС, а это возможно, только если М - цетр окружности (можно указать на равенство СК и КР, поэтому СМ = МС, и опять - М - центр)
Итак ,мы имеем ПРЯМОУГОЛЬНЫЙ треугольник АВС, угол АСВ = 90 градусов.
Из равенства дуг СВ и ВР (мы уже ДОКАЗАЛИ, что АВ - диаметр, пепендикулярный СР) следует, что угол СЕР в 2 раза больше ВСК,
то есть если считать угол ВСК = 5*х, то
угол ЕСР = 8*х, угол СЕР = 10*х.
Но угол ЕСР + угол СЕР = 90 градусов, откуда х = 5 градусов, угол САВ = угол КСВ = 5*х = 25 градусов, угол КВС = 90 - 25 = 65 градусов.
ответ углы треугольника 25, 65 и 90 градусов.
2. Сумма углов восьмиугольника вычисляется по формуле: 
. Разделив это число на 8, найдем чему равен один угол. 
. По определению, внешний угол это угол, смежный с любым внутренним. А так как сумма смежных углов равна 180 градусам, получаем: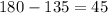 
, что и сходится с утверждением.
3. Разобьем параллелограмм на четыре треугольника путем проведения в нем диагоналей. Для произвольного треугольника на плоскости всегда выполняется неравенство треугольника: сумма длин двух сторон больше или равна длине третьей. Дальше все понятно, во вложении.
5. У правильного многоугольника с нечентым числом сторон осями симметрии являются прямые, выходящие из вершин углов, которые перпендикулярны противолежащей углам сторонам. Для правильного многоугольника точка пересечения этих прямых будет являться центром описанной окружности. А по свойству тех же правильных многоугольников, это точка будет еще и центром вписанной окружности. Следовательно, центр вписанной окружности является центром симметрии пятиугольника.
4√3 см
Объяснение:
За теоремою синусів
sinA/BC=sinB/AC
AC=BC*sinB/sinA=2√6 * √3/2 : √2/2 = 4√3 см