40-(15×2)=10
Объяснение:
периметр 40см
а две боковые по 15см
тогда мы от периметра отнимает две боковые стороны 40-(15×2)
или же просто 40-30=10 это и есть основание.
Из условия, что четыре ребра куба параллельны диагонали основания пирамиды, делаем вывод: вершины основания куба лежат на осях основания пирамиды, а 4 других вершины куба лежат на апофемах пирамиды.
Проведём осевое сечение пирамиды через 2 противоположные апофемы.
Куб рассечётся по диагонали, его сечение - прямоугольник. Пусть высота его равна "х", ширина как диагональ равна "х√2".
Из подобия треугольников сечения составим пропорцию:
(9 - х)/(х√2/2) = 9/2.
9х√2 = 36 - 4х,
х(4 + 9√2) = 36,
х = 36/(4 + 9√2) ≈ 2,152090371 .
ответ: длина ребра куба примерно равна 2,15.
1) Первый пункт задачи должен быть сформулирован так:
докажите, что все вершины четырехугольника АВСD лежат в одной плоскости, если его диагонали АС и ВD пересекаются.
Воспользуемся теоремой: через две пересекающиеся прямые можно провести плоскость и при том только одну.
Даны две пересекающиеся прямые АС и ВD. Проходящую через них плоскость обозначим α.
Прямая АС лежит в плоскости α, значит А∈α и В∈α.
Прямая ВD лежит в плоскости α, значит В∈α и D∈α.
Точки А, В, С, D принадлежат плоскости α, т.е. все вершины четырехугольника АВСD принадлежат плоскости α.
Что и требовалось доказать.
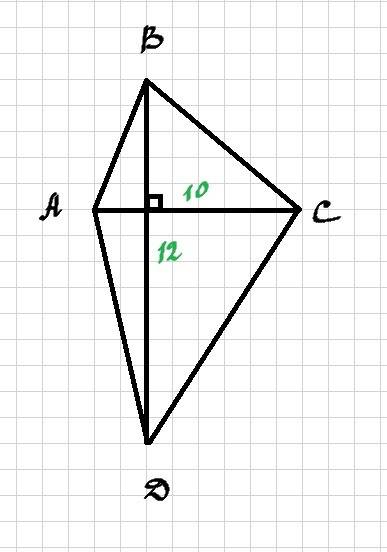
2) Рисунок к задаче прикреплен. Дан четырехугольник, у которого диагонали взаимно перпендикулярны и известны длины этих диагоналей (смотри рисунок).
Воспользуемся формулой для вычисления площади четырехугольника по двум диагоналям и углу между ними.
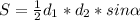, где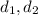 
– диагонали четырехугольника, 
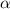– угол между диагоналями.
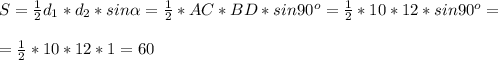
ответ: площадь АВСD равна 60 см².
10cм
Объяснение:
40-(15+15)=10