Дано :
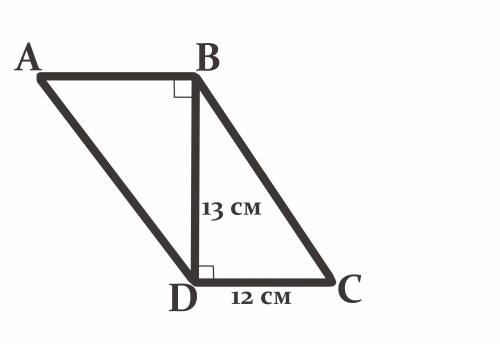
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
1. Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
2. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
Эти свойства изучают в 8 классе, когда проходят тему подобных треугольников, из подобия двух прямоугольных треугольников их и выводят. Высота в прямоуг. треугольнике, выходящая из вершины прямого угла, делит гипотенузу на отрезки, один из них - проекция одного катета, другой - проекция другого.