AOD подобен BOC, значит, раз отношение площадей равно квадрату коэффициента подобия, BC/AD = 4/5. Пусть АD=x, тогда BC=4/5 x. Проведем из О перпендикуляры к основаниям: ОК - перпендикуляр к ВС, ОF - перпендикуляр к AD. Пусть ОК=n, ОF=m
16=Площадь ВОС= 1/2 ОК * ВС = 1/2 n 4/5 x = 2/5 xn, откуда xn = 40
25=Площадь AOD=1/2 OF * AD = 1/2 mx, откуда mx=50
Высота трапеции равна m+n
Площадь трапеции равна произведению полусуммы оснований на высоту
сумма оснований 9/5 x
Площадь трапеции 9/5 х * 1/2 * (m+n) = 9/10 *(xm + xn) = 9/10 (40 + 50) = 81
Пусть меньшая сторона параллелогамма равна а, высота, проведенная к этой стороне равна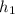 
, а острый угол между сторонами параллелограмма равен 
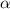. Большая сторона параллелограмма пусть равна b, высота, проведенная к этой стороне равна 
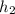. По условию задачи 
.
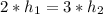То есть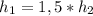 
. Если вычислить площадь параллелограмма, то по одной из формул будет
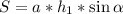или 
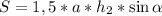. Попробуем вычислить площадь параллелограмма через другую сторону и высоту
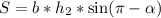. Или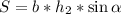 
.
Приравняем два полученных выражения площади
.
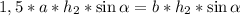Получается, что
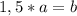
Так как по условию задачи периметр параллелограмма равен 60 см, то
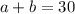
Используя что 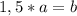, получаем
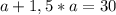
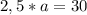
а=12. Тогда b=1,5*a, b=18 см.
Значит большая сторона параллелограмма равна 18 см.
Площадь основания считается по формуле Герона: a = 15; b = 16; c = 17;
p = (a + b + c)/2 = 24; p - a = 9; p - b = 8; p - c = 7;
S = корень(24*9*8*7) = 24*корень(21);
Площадь боковой поверхности в данном случае проще всего сосчитать по формуле
Sбок = S/cos(60) = 48*корень(21); площадь полной поверхности 72*корень(21).
Если надо -
доказать формулу Sбок*cos(Ф) = S, если все грани наклонены под одним углом, просто, если представить площадь основания как сумму площадей проекций боковых граней. Ясно, что у каждой боковой грани в качестве проекции - треугольник, у которого общее с гранью основание - это ребро основания пирамиды, а отношение высот как раз равно cos(Ф). Кроме того, при равных углах наклона боковых граней вершина пирамиды проектируется в центр вписанной окружности, поскольку эта проекция будет равноудалена от сторон оснований. Это означает, что все АПОФЕМЫ равны. И - само собой, доказывает необходимую формулу - достаточно просто сложить площади всех проекций боковых граней.