Площадь прав тр через радиус вписанной окружности равен 3 корня из 3 на радиус в квадрате, а площадь вписанного круга равна Пи на радиус в квадрате.
Рассмотрим во сколько раз площадь треугольника больше площади круга. ![\frac{3 \sqrt[]{3}r^{2}}{\pi r^{2}}=\frac{3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/07e0a.png)
Пусть площадь круга х, тогда площадь треугольника (по условию) ![x+27\sqrt[]{3}-9\pi](/tpl/images/0144/4450/08b8d.png) с одной стороны и
с одной стороны и ![\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/56410.png) с другой.
с другой.
Получим уравнение ![x+27\sqrt[]{3}-9\pi=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/99a9d.png)
Разрешим относительно х. Приведем к знаменателю Пи и приравняем числители
![\frac{x\pi}{\pi}+\frac{\pi27\sqrt[]{3}}{\pi}-\frac{9\pi^{2}}{\pi}=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/4f04e.png)
![x\pi}+\pi27\sqrt[]{3}-9\pi^{2}=x3 \sqrt[]{3}](/tpl/images/0144/4450/57c86.png)
Вынесем 3 корня из трех - Пи за скобки и получим
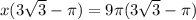
площадь круга = 9Пи
Найдем радиус круга
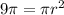
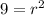
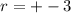
Т к радиус не может быть отрицательным то он равен 3
у - х = 0, у + х = 0, у - 2х + 4 = 0
y = x, y = - x, y = 2x - 4
Пусть прямые у = х и у = 2х - 4 пересекаются в точке А,
а прямые у = - х и у = 2х - 4 - в точке В.
Прямые у = х и у = - х пересекаются в начале координат и взаимно перпендикулярны.
Найдем координаты точки А:
у = х
у = 2х - 4
2x - 4 = x
x = 4
y = 4
A(4 ; 4)
Найдем координаты точки В:
у = - х
у = 2х - 4
2x - 4 = - x
3x = 4
x = 4/3
y = - 4/3
B(4/3; - 4/3)
AO = √(4² + 4²) = √32 = 4√2
BO = √((4/3)² + (4/3)²) = √(16/9 + 16/9) = √(32/9) = 4√2/3
Saob = 1/2 AO · BO = 1/2 · 4√2 · 4√2/3 = 16/3
Объяснение:
1. Нехай бічна сторона х (см), тоді основа х + 4 (см)
Якщо периметр дорівнює 22 см, то маємо рівняння
x+x+x+4=22
3x=18
x=6
Тоді дві бічні сторони дорівнюють по 6 см, а бічна сторона 6+4 = 10 см.
2. Завтра допишу, бо вже пізно