2*16.8=33.6
Объяснение:
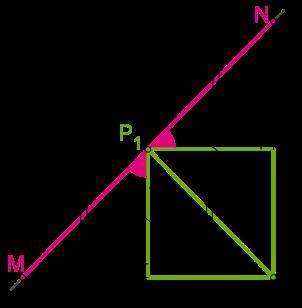
1. Через точку конца диагонали квадрата проведём прямую MN перпендикулярно диагонали. Тогда со сторонами квадрата и прямыми, на которых находятся стороны квадрата, проведённая прямая образует углы 45°. Это легко доказать с чертежа в приложении. Только вместо точки Р у нас Д.
2. Теперь имеем 4 равных прямоугольных треугольника (признак по равным катетам и острым углам), у которых равны их гипотенузы.
3. Отрезок MN состоит из гипотенуз двух треугольников, следовательно, длина MN=2⋅16,8=33,6 ед. изм.
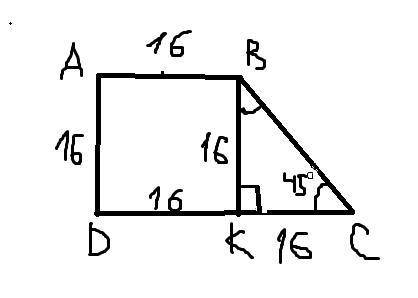
ответ:Большее основание равно 32 см.
Объяснение: Рассматриваем трапецию ABCD - прямоугольная (чтобы было понятней: AB - меньшее основание, DC - большее основание, угол С=45°). Проведём высоту BK к большему основанию из вершины угла B. Получили прямоугольник ADBK. По свойству противоположных сторон BK=AD=16см, AB=DK=16см. Теперь рас-м треугольник BCK - прямоугольный. Т. к. угол C=45°, то найдём угол КВС: (сумма углов тр-ка - 180°) 180°-(90°+45°)= 45°. Следовательно, тр-к BCK -равнобед-й, ВК=СК=16см. DC = DK+KC=16+16=32СМ.
1-ая задача:
вкратце)
расстояние- это перпендикуляр
поэтому треугольник АВН прямоугольный.(Н- точка расстояния от М до АВ)
угол САМ равен МАН(т.к. АМ бисс)
АМ- общая сторона
из этого АСМ=АМН(треугольники)
из чего СМ=МН=7см
ответ:7см
2-ая задача:
Любая точка биссектрисы неразвёрнутого угла равноудалена от сторон этого угла.
Доказательство:
Рассмотрим треугольники BFK и BFP.
∠BKF=∠BPF=90º, ∠KBF=∠PBF (так как по условию BD — биссектриса ∠ABC).
BF — общая сторона.
Значит, ∆BFK=∆BFP (по гипотенузе и острому углу).
Из равенства треугольников следует равенство соответствующих сторон: FK=FP.
Что и требовалось доказать.