5.2. Если прямая  перпендикулярна двум пересекающимся прямым (АВ и АС) , лежащим в одной плоскости ( пл. треугольника АВС) , то эта прямая
перпендикулярна двум пересекающимся прямым (АВ и АС) , лежащим в одной плоскости ( пл. треугольника АВС) , то эта прямая 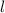 перпендикулярна самой плоскости ( пл. ΔАВС).
перпендикулярна самой плоскости ( пл. ΔАВС).
в) Прямая 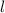 перпендикулярна плоскости треугольника АВС.
перпендикулярна плоскости треугольника АВС.
5.3. Так как КО⊥ АВСД ( плоскости параллелограмма АВСД) , то эта прямая перпендикулярна ЛЮБОЙ прямой, лежащей в плоскости АВСД. Значит, КО⊥АВ , КО⊥ВС , КО⊥АД , КО⊥СД , КО⊥АС , КО⊥ВД ,...
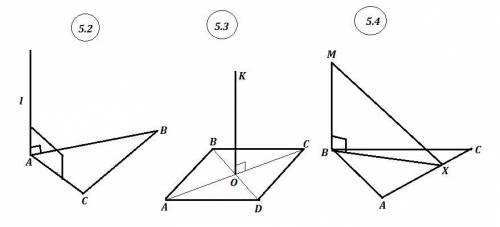
5.4. МВ⊥пл ΔАВС ⇒ МВ перпендикулярна ЛЮБОЙ прямой, лежащей в этой плоскости АВС, в том числе МВ⊥ВХ ( Х∈АС⊂ΔАВС ) ⇒
∠МВХ=90° и ΔМВХ - прямоугольный .
Cм. рисунки.
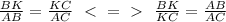
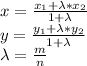
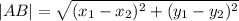
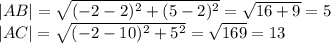
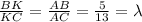
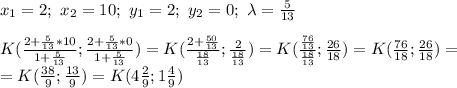
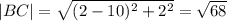
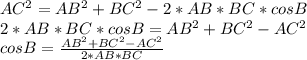
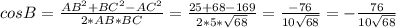
 треугольник тупоугольный
треугольник тупоугольный
это верно да это паралейка