Площадь боковой поверхности пирамиды – сумма площадей боковых граней.
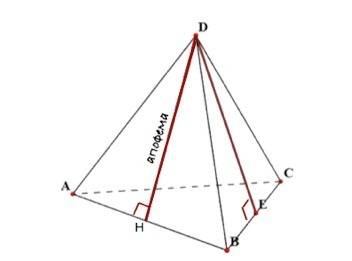
В правильной пирамиде все боковые грани рввны и являются равнобедренными треугольниками, а высота боковой грани называется апофемой.
S (грани)=a•h:2
S=8•10:2=40 см²
Таких граней три.
S=40•3=120 см²
--------
Или: Площадь боковой поверхности правильной пирамиды равна произведению апофемы на полупериметр основания
S=h•(a•3:2)=10•8•3:2=120 см²
---------
Примечание:
В правильном многоугольнике тоже есть апофема - так называется отрезок (а также его длина) перпендикуляра, опущенного из центра правильного многоугольника на любую из его сторон.
ответ:1 }S1=1/2*a*a*sin60
2} S2=p*h=3a*h 3} S=2*S1+S2 4} V=S1*h
Объяснение: