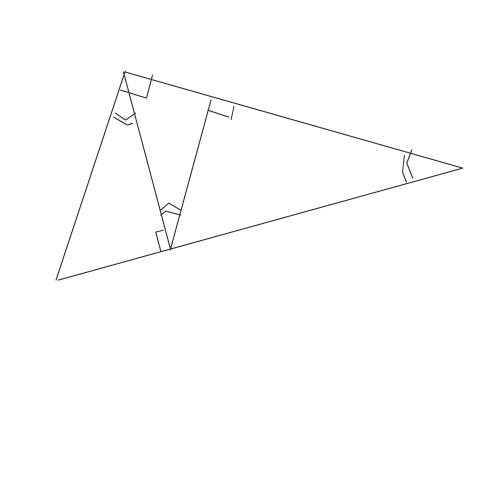
Нарисуйте прямоугольный треугольник. Из вершины прямого угла опистите высоту к гипотенузе. Получите 2 подобных треугольника из одного ( исходный не считаем). Затем из основания высоты ( из вершины прямого угла треугольника, который получился при делении) проведите высоту к его гипотенузе ( она же катет исходного треугольника).
Каждый из двух прямоугольных треугольников, на которые делится исходный треугольник высотой, опущенной из прямого угла на гипотенузу, подобен исходному по двум углам: один угол общий, а другой угол прямой.
a)Около квадрата всегда можно описать, в квадрат всегда можно вписать окружность. Почему? /если сумма противоположных сторон четырехугольника равна сумме других противоположных сторон, то в него можно вписать окружность/, а если суммы противоположных углов четырехугольника равны, около него можно описать окружность. Квадрат обладает и тем, и другим свойством.
б)Около любого треугольника можно описать окружность, центр ее находится в точке пересечения серединных перпендикуляров, в любой треугольник можно вписать окружность, центр ее лежит на точке пересечения биссектрис внутренних углов треугольника.
ИСХОДЯ ИЗ ВЫШЕСКАЗАННОГО
в) В ромб можно вписать окружность, а описать нельзя
г)Около параллелограмма нельзя описать, или вписать в него окружность;
д) около прямоугольника можно описать окружность, центр ее совпадает с точкой пересечения диагоналей. Вписать окружность в прямоугольник нельзя
е) Около равнобедренной трапеции можно описать окружность, т.к. суммы противоположных углов равны . В равнобокую трапецию можно вписать окружность, только в случае выполнения условия, если сумма оснований равна сумме боковых сторон трапеции.