1.
По теореме косинусов найдём угол MON
MN² = OM² + ON² - 2*OM*ON*cos(∠MON)
12² = 20² + 20² - 2*20*20*cos(∠MON)
144 = 400 + 400 - 800*cos(∠MON)
656 = 800*cos(∠MON)
cos(∠MON) = 41/50
∠MON = arccos(41/50)
2.
Площaдь треугольника MON
S(ΔMON) = 1/2*OM*ON*sin(∠MON)
sin(∠MON) = √(1-cos²(∠MON)) = √(1 - 41²/50²) = √(2500 - 1681)/50 = √819 / 50 = 3√91/50
S(ΔMON) = 1/2*20*20*3√91/50 = 12√91
3.
Площадь кругового сектора MON
S(∪MON) = ON²*∠MON/2 = 20²/2*arccos(41/50) = 200*arccos(41/50)
4.
Площадь заштрихованной фигуры
S = S(∪MON) - S(ΔMON) = 200*arccos(41/50) - 12√91 ≈ 7.404
68. По данным на рисунке найдите площадь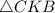 
.
ΔСКВ - прямоугольный (∠С = 90°).
СК - высота (СК⊥АВ).
АК = 4, КВ = 16.
Найти :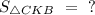
Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно,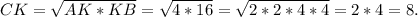 
Следовательно,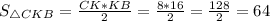 
ед².
64 ед².
- - -70. ABCD - прямоугольник. Найдите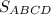 
.
Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :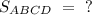
Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно,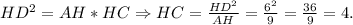 
Следовательно,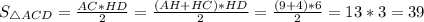 
ед².
Тогда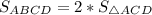 
= 2*39 ед² = 78 ед².
78 ед².
АС = BD,AD = BCи ∟DAB = ∟CBА