а) Векторы ВВ1 и В1С совпадают с катетом и гипотенузой прямоугольного треугольника BВ1С, следовательно, ВВ1С=45°.б) BD = B1D1 , т.к. они сонаправлены и имеют одинаковую длину. BD = B1D1 =- DB .Угол между DB и DA — угол между стороной и диагональю квадрата, т.е. α=45°. Тогда угол междуDA и B1D1 равен 135°.в) A1C1 и A1B совпадают со сторонами равностороннего треугольника АВС и отложены из одной точки. Следовательно, угол 60°.г)(угол между стороной и диагональюквадрата).д)е)Пусть О — точка пересечения диагоналей В1С и ВС1,квадрата ВВ1С1С.следовательно,ж)следовательно,з)следовательно, угол между ними равен 180°Не знаете как решить? Можете с решением? Заходите и спрашивайте.
Хорошо, сведем задачу к нахождению диагонали трапеции т.к. есть формула S= d^2/2 * sinA где d- диагональ, синус угла 60 у нас есть он равен 1/2* корень из 3. Диагонали в равнобедр. трапеции образуют собой равнобедр. треугольники AOD и BOC рассмотри треугольник ВОС: угол ВОС равен 180- 60= 120, тогда углы при основании равны по 30 (углы ОСВ и ОВС) далее возьмем прямоугольный треугольник АНС где АН- высота: угол АСН мы нашли он равен совпадающему углу ОСВ и равен 30 тогда угол НАС равен 180-90-30=60 АН=2 найдем сторону НС: по формуле НС = АН*tgА= 2* tg HAC= 2 * tg 60 = 2* корень из 3= 2 корня из 3 окей, далее найдем АС она же является диагональю трапеции: АС= НС/sin НАС= 2 корня из 3/ ( 1/2* корень из 3) = 4 готово, осталось посчитать: S = АС^2 /2 * sin 60= 8* корень из 3 /2 = 4 корня из 3 см в квадрате
Объяснение:
a) a/sin60°=2R (теорема синусов)
сторона a = 2Rsin60°=12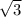
/2=6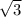
б) r = 0,5 a/√3 = 3
в) SΔ =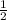
a²sin60°=54√3/2=27√3