Геометрия: Жаратылыстану 6сынып 4тоқсан 5тапсырма

Жаратылыстану 6сынып 4тоқсан 5тапсырма

👇

Увидеть ответ

Ответ:

денисПрекрасный

17.04.2023

ответ:айтыңдарщы

Объяснение:

Бондаршы

4,4(55 оценок)

Открыть все ответы

Ответ:

alskdjfhg123a

17.04.2023

Задача 1

Решение(согласно моему рисунку)

1) Проведем высоту ВН.

2) Рассмотрим четырехугольник АВНД

Он будет параллелограммом, т.к. АВ || СД (как основания), а АД || ВН (т.к. высоты к одной стороне)

Тогда, т.к. АВНД - параллелограмм, АВ=ДН=6 см., АД=ВН (по св-ву параллелограмма)

3) Рассмотрим прямоугольный треугольника ВНС

НС=10 - 6=4 см.

Угол С=60° (по условию)

Тогда угол НВС=90° - 60°=30°.

В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузы. Гипотенуза ВС=8 см. (это и будет большая боковая сторона)

ВС²=ВН² + НС² (теорема Пифагора)

ВН²=64 - 16

ВН²=48

ВН=4√3

4) ВН=АД=4√3, тогда АД=4√3 (это и будет меньшая боковая сторона)

ответ: АД=4√3 см., ВС=8 см.

4,7(63 оценок)

Ответ:

Xylophone

17.04.2023

Так как AK - биссектриса, то:
$\frac{BK}{AB}= \frac{KC}{AC} \ \ \textless \ =\ \textgreater \ \ \frac{BK}{KC}= \frac{AB}{AC}$
при делении точкой отрезка на 2 части, относящиеся как m к n, есть формула для вычисления координат этой точки:
$x= \frac{x_1+\lambda*x_2}{1+\lambda} \\y= \frac{y_1+\lambda*y_2}{1+\lambda} \\\lambda= \frac{m}{n}$
ищем длины AB и AC:
используем формулу:
$|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
$|AB|=\sqrt{(-2-2)^2+(5-2)^2}=\sqrt{16+9}=5 \\|AC|=\sqrt{(-2-10)^2+5^2}=\sqrt{169}=13$
$\frac{BK}{KC}= \frac{AB}{AC}= \frac{5}{13} =\lambda$
находим координаты точки K:
$x_1=2;\ x_2=10;\ y_1=2;\ y_2=0;\ \lambda=\frac{5}{13} \\ \\K( \frac{2+ \frac{5}{13}*10 }{1+\frac{5}{13}} ;\frac{2+ \frac{5}{13}*0 }{1+\frac{5}{13}})=K( \frac{2+ \frac{50}{13} }{ \frac{18}{13}}; \frac{2}{ \frac{18}{13} })=K( \frac{ \frac{76}{13} }{ \frac{18}{13}}; \frac{26}{18} )=K( \frac{76}{18}; \frac{26}{18}) = \\=K( \frac{38}{9}; \frac{13}{9})=K(4 \frac{2}{9};1 \frac{4}{9} )$
теперь определим вид треугольника для этого используем теорему косинусов:
для начала найдем длину BC:
$|BC|=\sqrt{(2-10)^2+2^2}=\sqrt{68}$
вид треугольника будем определять по косинусу самого большого угла; если cos<0, то угол тупой; если cos=0, то угол прямой; если cos>0, то угол острый.
Против большей стороны лежит больший угол, поэтому запишем теорему косинусов для AC и косинуса угла B
$AC^2=AB^2+BC^2-2*AB*BC*cosB \\2*AB*BC*cosB=AB^2+BC^2-AC^2 \\cosB= \frac{AB^2+BC^2-AC^2}{2*AB*BC}$
подставим значения:
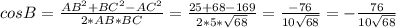
$cosB= \frac{AB^2+BC^2-AC^2}{2*AB*BC}= \frac{25+68-169}{2*5*\sqrt{68}}= \frac{-76}{10\sqrt{68}} =- \frac{76}{10\sqrt{68}}$
cosB<0 поэтому угол тупой и треугольник тупоугольный
ответ: $K(4 \frac{2}{9};1 \frac{4}{9} );\$ треугольник тупоугольный