сторона = 8 см
площадь = 40,74 см²
Объяснение:
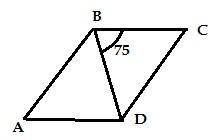
1. BC -6 см, BD - 7 см. CD - ?
Вторую сторону параллелограмма CD находим по теореме косинусов:
CD² = BC² + BD² - 2 * BC * BD * Cos B
По таблице Брадиса примем значение косинуса 75° = 0,25
CD² = 36 + 49 - 2 * 6 * 7 * 0.25 = 64
CD = 8
2. Площадь треугольника ВСD - это 1/2 площади параллелограмма ABCD. Найдем S Δ ВСD через синуса угла B и умножим ее на 2.
S Δ ВСD = 1/2 * BC * BD * Sin 75, ⇒ S ABCD = BC * BD * Sin 75
Sin 75 по таблице Брадиса примем 0,97
S ABCD = 6 * 7 * 0.97 = 40.74 см²
Дано :
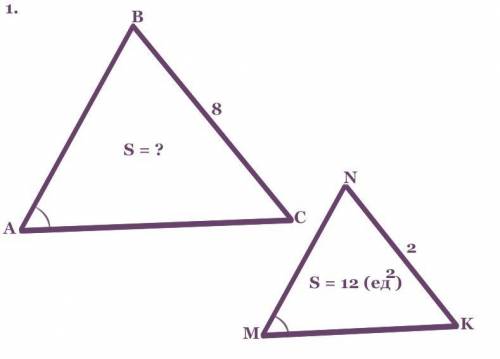
ΔАВС ~ ΔMNK.
∠А = ∠М.
ВС = 8.
NK = 2.
S(ΔMNK) = 12 (ед²).
Найти :
S(ΔABC) = ?
В подобных треугольниках против равных углов лежат сходственные стороны.Отсюда стороны ВС и NK - сходственные.
Отношение сходственных сторон равно коэффициенту подобия.То есть -
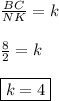
Но заметить, ища коэффициент подобия, я ставила в числитель элемент бóльшего треугольника. Поэтому при дальнейших расчётах, я буду также ставить элементы/площадь бóльшего треугольника в числитель.
Площади подобных треугольников относятся как квадрат коэффициента подобия.Отсюда -
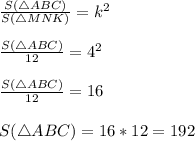
192 (ед²).
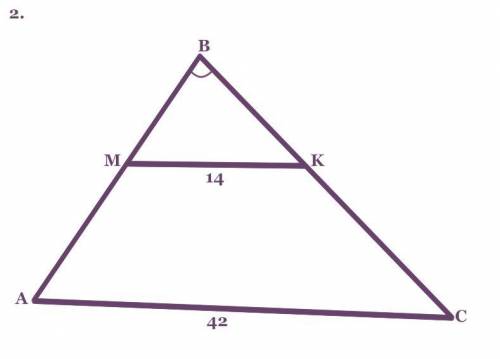
- - -2. В треугольнике АВС отрезок MК (М ∈ АВ, К ∈ ВС) параллелен АС. МК = 14, АС = 42. Периметр треугольника МВК равен 32. Найдите периметр треугольника АВС.- - -Дано :
ΔАВС.
М ∈ АВ, К ∈ ВС.
МК ║АС.
МК = 14.
АС = 42.
Р(ΔМВК) = 32.
Найти :
Р(ΔАВС) = ?
В треугольнике параллельный одной из сторон треугольника отрезок, пересекающий две другие стороны треугольника в точках, отсекает от данного треугольника подобный треугольник.Отсюда -
ΔАВС ~ ΔMBK.
В подобных треугольниках против равных углов лежат сходственные стороны. И их же отношение равно коэффициенту подобия.∠В - общий для ΔАВС и ΔMBK.
Отсюда стороны МК и АС - сходственные.
Тогда -
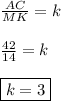
Отсюда -
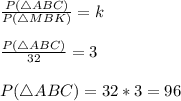
96.
Знайти: P
Нехай, гіпотенуза ВС = х, тоді АВ=х-2, АС = х-9
За т . Піфагора: BC² = АВ²+АС²
х²=(х-2)²+(х-9)²
х²=х²-4х+4+х²-18х+81
х²=2х²-22х+85
х²-22х+85 = 0
D = 484-340=144
x1=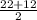 = 17
= 17
x2=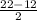 = 5
= 5
х2 не задовільняє умові задачі, так як, в такому випадку АС буде з мінусовим значенням, а це неможливо
Отже, AB = 15, AC = 8, BC = 17
P = AB + AC + BC = 15+8+17=40 см
Відповідь: Р=40 см